CS 131 – Problem Set 3
Problems must be submitted by Monday February 19, 2024 at 11:59pm, on Gradescope.
Where to submit: Create an account on https://gradescope.com using your bu.edu email address. You’ll find yourself already enrolled in CS 131 on gradescope. If not, use code BBZJP8 to add yourself to the class.
What to submit: You will be submitting a .pdf file with your write up into the gradescope assignment PS3.
Problem 1. [20 points] Let x and y be integers. Prove (with a direct proof) that if x + y is even then x 2 + y 2 is even.
Problem 2. [20 points, 10 points each]
a) Prove that a 2 ≥ a whenever a is a natural number using proof by cases. Hint: You have two cases: (1) a = 0 and (2), a ≥ 1
b) Prove that if a ≥ 0 and b ≥ 0 then their geometric mean, √ab, is at least as large as min(a, b). Remember “without loss of generality”. You can use the fact that √· is increasing (i.e. if x ≤ y then √x ≤ √y).
Problem 3. [20 points, 10 points for each part] Recall the definition of absolute value:
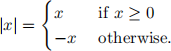
a) Prove that |x| = | − x| for all real numbers.
b) Prove that |x − y| = |y − x|.
Problem 4. [10 points] Prove or disprove the following statements:
a) [3 points] There exists a unique natural number x such that x2 = x.
b) [3 points] The product of two irrational numbers is always irrational.
Hint: You can use the fact √2 is irrational
c) [4 points] The sum of two irrational numbers is always irrational.
Problem 5. [30 points] Recall that the definition of perfect square:
A real number x is a perfect square if and only if there exists an integer y such that such x = y2.
Prove that if n is a perfect square, n + 2 is not a perfect square.
Hint: Use contradiction, then go by cases. There will be four cases and you will need to reach a contradiction in each case.