Bayesian Inference and Computation
Tutorial Problems 1
These exercises provide some practice in performing basic Bayesian analyses.
1) Water consumption

In the Melbourne average daily per capita water use analyis, we modelled the discrete observa- tions x1 ,..., xn as independent draws from a Poisson(θ) distribution. Assuming a Gamma(α,β) prior, which has a density function of

we computed the posterior as a Gamma  distribution.
distribution.
(a) Show that the posterior mean of θ is given by  .
.
(b) Show that the posterior variance of θ is given by  .
.
(c) Show that the predictive distribution for a future observation, y, is
NegBin 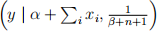 , where the probability mass function of a Negative Bino- mial random variable with parameters a > 0, and 0 ≤ p ≤ 1, is given by
, where the probability mass function of a Negative Bino- mial random variable with parameters a > 0, and 0 ≤ p ≤ 1, is given by

2) Rock Strata

(a) Rock strata A and B are difficult to distinguish in the field. Through careful laboratory studies it has been determined that the only characteristic which might be useful in aiding discrimination is the presence or absence of a particular brachiopod fossil. In rock exposures of the size usually encountered, the probabilities of fossil presence are found to be as in the table below. It is also known that rock type A occurs about four times as often as type B in this area of study.

If a sample is taken, and the fossil found to be present, calculate the posterior distribution of rock types.
(b) If the geologist always classifies as A when the fossil is found to be present, and classifies as B when it is absent,what is the probability she will be correct in a future classification?
3) Coloured Balls

(a) Repeat the Coloured Balls example from Lecture 1, using a different choice of prior distribution. In what way does this change of prior affect the posterior probability of no black balls left in the bag?