Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
MATH39512 Survival Analysis for Actuarial Science: example sheet 6
*=easy, **=intermediate, ***=difficult
* Exercise 6.1
Consider the following survival data of a group of patients who were under observation for some period of time:
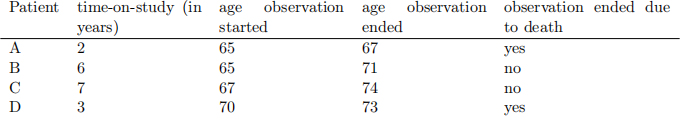
Here all the patients started to be observed at the same time and the time-on-study means the amount of time a patient was under observation. The survival time of interest is the time until death. Assuming a Cox PH model, find an expression for the partial likelihood in terms of the multipliers of the patients (i.e. your answer should be of the same form as in Example 4.3 in the notes) in the case where
(a) time-on-study is the time scale;
(b) the age of the patient is the time scale.
** Exercise 6.2
The recorded survival times, in years, of six patients following a heart bypass operation are given below.
10.4+, 6.6, 4.2, 6.2+, 15.9, 6.3,
where values followed by a + indicate right censored survival times. Also recorded for each patient is x, the number of cigarettes smoked on average per week prior to the operation. These are, respectively,
0, 100, 60, 0, 0, 40.
(a) Assume a Cox proportional hazards model with single covariate 儿 and let β be the regression coefficient of x. Find an explicit expression in terms of β for the partial likelihood in this model.
Numerical maximisation of LP(β) yields a maximum likelihood estimate βˆ = 0.017 and a maximised partial likelihood value LP(βˆ) = e−3.439 .
(b) What is the interpretation of the value βˆ in terms of the effect of smoking on the future lifetime of a patient who undergoes heart bypass operation?
(c) We wish to test the hypothesis H0 that the number of cigarettes smoked does not have an effect on the distribution of the future lifetime of heart bypass patients. Still assuming a Cox proportional hazards model, perform (i) the score test and (ii) the likelihood ratio test.
* Exercise 6.3
(a) Set up a Cox PH model to model the mortality of a group of policyholders where the time scale is age and with covariates indicating (i) the gender of the policyholder, (ii) his/her health status modelled as an index between 1 and 10 where 1 represents very healthy and 10 very unhealthy and (iii) whether the policyholder has bought an assurance or an annuity.
(b) What sign would you expect the regression coefficient to have that corresponds to the health status?
(c) Explain why it makes sense for an insurance company to include covariate (iii) into the model?
*** Exercise 6.4
In an observational hip replacement study the time to revision of the prosthesis was analysed by a Cox proportional hazards model with two categorical covariates/factors. The table below gives the estimates for the regression coefficients corresponding to the two covariates and their standard errors (i.e. asymptotic standard deviations). The (asymptotic) covariance between the two coefficients was estimated to be −0.00163.

(a) Give a 95% confidence interval for
(i) the hazard ratio of a male relative to a female, both individuals having the same hip surgery history;
(ii) the hazard ratio of somebody who had hip surgery relative to somebody who did not have previous hip surgery, both individuals being of the same gender.
(b) (i) Calculate the hazard ratio for a male with previous hip surgery compared to a female without previous hip surgery.
(ii) Give a 95% confidence interval for this hazard ratio and interpret it.
(c) The data have been collected over three decades. Do you see any problems arising from this? Give a reason. If yes, how can you address them in the analysis?
*** Exercise 6.5
Consider the Cox PH model with one covariate and assume that this covariate is categorical. Let β be the corresponding regression coefficient. Show that with the partial likelihood approach and under the assumption that no individuals fail at the sametime, the score test for testing H0 : β = 0 versus HA : β 0 is equivalent to the log-rank test as defined in Definition 2.8 with t0 = τR .