ECON5102
MACROECONOMICS
Term 1, 2024
ASSIGNMENT 1
DUE: 5pm Friday, 8 th of March 2024
Academic Honesty
Academic honesty is a core value of the University, and all students are required to act honestly, ethically and with integrity. The consequences of engaging in plagiarism and academic dishonesty, along with the process by which they are determined and applied, are set out in the Student Misconduct Procedure. Under the same policy, as the lecturer, I must report any suspected plagiarism or academic dishonesty.
Instructions
• This is an individual assignment which accounts for 10% of your final grade. You may discuss with your classmates, but please ensure that the submitted work is independent.
• You can either hand-write or type your answers (or both), but please compile all your answers in one PDF file and submit it via Moodle. You can only submit your work once, so please double check before you submit. The page limit of the submission is 10 pages including appendix (a penalty will apply if the page limit is exceeded).
• There are 3 questions (with sub-questions) in this assignment, and please attempt all questions. Detailed solutions to each question will be provided during seminars after the assignment is due.
• I will randomly select 4 sub-questions (same 4 sub-questions for everyone) to grade, and each question is worth 2.5 points. The total point of this assignment is 10. The grading will be based on the completion and general quality of your submission.
• For all questions, please show your derivations. Answers without intermediate steps will be considered incomplete.
• Based on the University late policy, a late submission is subject to a penalty of 5% (of the total points) per calendar day. No submissions will be accepted after Tuesday (12/04) 6pm.
• Make sure to include a cover sheet to your submission. They can be found on Moodle.
QUESTIONS
1. You work as an analyst at the World Bank, and you have been granted access to a large dataset containing information on GDP per capita for several countries since 1990. Your direct manager asks you to study the data and prepare for some questions other analysis might have about long-term economic growth.
To access the data, visit the Word Bank’s website (https://data.worldbank.org/) and collect data on GDP per capita (PPP, constant 2017 international $) for all countries in their dataset. Make sure to collect data for all years they have available. Download the data on Microsoft Excel (or equivalent) and remove all years until 1989 (keep 1990 onwards). The dataset includes information on regions also (e.g., Arab countries, Low Income, Euro Area). Be mindful of those when answering the questions.
The most pertinent questions the analysts at the Bank sent to you are below. Answer all of them to the best of your ability.
1.1) Which country had the highest GDP per-capita in 2022? Which country had the lowest? What was the value for Australia?
1.2) Which country had the highest average growth rate of GDP per capita in the last 10 years from 2022 (i.e., from 2012 until 2022 inclusive)? Notice that some countries may not have enough data to obtain this information. Ignore these cases. Hint: use equation (3.9) of the textbook with t = 10.
1.3) Using the average growth rate for China and India, indicate how many years would these countries take to “catch up” to the level of GDP per capita for Australia. Assume that Australia does not grow over the years.
1.4) Repeat the exercise above assuming Australia grows at its average rate.
1.5) Provide a brief description of what the rule of 70 is. Create a similar rule to indicate how many years would the economies of China, India and Australia take to triple their sizes, using their 10-year average growth rate calculated in (1.2).
2. Let’s investigate the Solow-Swan model for when the population is allowed to grow at the constant rate n > 0. We will use a Cobb-Douglas production function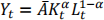 
with α not being equal to 1/3.
The per-capita equation describing the behaviour of capital over time now changes to kt+1 =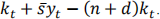 
Notice that small letters in this equation refer to per-capita terms, e.g., Kt = Kt/Lt.
2.1) What is the interpretation of α and (1 − α) in this model?
2.2) Find the expression for production function in per capita terms. Plot a graph with the production function, savings function and depreciation function, all in per capita terms. Clearly label all curves and axes.
2.3) Find the expression for output per worker (y) at the steady state. Hint: the definition of steady state is the point at which capital per worker does not grow.
2.4) In 2021, Australia had a GDP per capita level of around $49,609, while Chile’s was about $25,412. Using the result you found in (2.2), give two reasons that could explain why these two countries have very large differences in standard of living.
2.5) Find the expression for consumption per capita at the steady state in this economy. Compare this case to the one when the population does not grow (n = 0).
3. Answer the following questions about the Romer model.
3.1) What is the motivation to study the Romer model? I.e., what are some of the issues the Solow-Swan model had that stimulated economists to look for an alternative? Explain using at most 3 sentences.
3.2) What does it mean for a good to be non-rival? How is it different from an excludable good? Explain using at most 3 sentences.
3.3) Why is the Romer model incompatible with perfectly competitive markets? Justify using at most 3 sentences.
3.4) Why do we not talk about the notion of steady state in the Romer model? Is it possible for the steady state to be observed in the Romer model? Explain using at most 3 sentences.
3.5) You are the finance minister to a country whose economy works exactly like in the Romer model we considered in lectures. The prime minister summons you to their office asking if there is a way to increase economic growth permanently without sacrificing output in the short run. Provide one recommendation of how this could be achieved. Make sure to include (i) the economic intuition; (ii) a diagram illustrating the dynamics of GDP per capita over time; and (iii) some equations to further support your suggestion.