CSC318/M18 First Coursework
March 2024
Instructions.
• The coursework is to be solved in groups of 2-4.
• Submission deadline: Friday, 22nd March 2023, 11:00am GMT. Late submis-sions will not be considered.
• Submissions must be made through Canvas in PDF format.
• Make sure to submit the correct version of your document. We will not consider any “corrections” to your submission after the submission deadline.
• Clearly state the names and student numbers of all group members at the beginning of the document.
• Only one group member should submit a document on behalf of the whole group. If more than one group member submits a document, you will lose 5 marks for each extra submission.
Academic Integrity.
By submitting coursework, electronically and/or hardcopy, you state that you fully understand and are complying with the University’s policy on Academic Integrity and Academic Misconduct. The policy can be found at https://myuni.swansea.ac.uk/academic-life/academic-misconduct. The consequences of commit-ting academic misconduct can be extremely serious and may have a profound ef-fect on your results and/or further progression. The penalties range from a written reprimand to cancellation of all of your marks and withdrawal from the Univer-sity.
Part I - Public Key Cryptography
Problem 1.
Generate an RSA key pair using the modulus n = pq where p = 29 and q = 41. Use the public/encryption exponent e = 611. Sign the message m = 11 using the private/decryption exponent. [20 marks]
Problem 2.
Alice and Bob are performing a Diffie-Hellman key exchange using the base g = 7 and the modulus p = 211. Alice has sent the public element A = 124. Bob has sent the public element B = 119. Without the help of a computer or calculator, find Alice’s and Bob’s shared secret! To avoid excessive calculations, you may use the table below, which lists some powers of 7 and 124 modulo 211. Give a brief overview of the method you have used – do not show intermediate results of standard calculations.

Hint. Do not attempt to brute-force the discrete logarithm problem (directly). [20 marks]
Part II - Symmetric Key Cryptography
In the next three problems you are asked to perform known-plaintext attacks on certain symmetric ciphers that can be found in the Java code for the coursework. For each of the ciphers described below, your task is the same. You are given a plaintext, contained in the file
files/$NAME/Known Plaintext ($NAME).txt.
This plaintext was encrypted into the ciphertext contained in the file
files/$NAME/Known Ciphertext ($NAME).txt.
The ciphertext contained in the file
files/$NAME/Unknown Ciphertext ($NAME).txt
was encrypted with the same key. Your task is to find the plaintext corresponding to the unknown ciphertext. In the above, $NAME ∈ {Einstel,Zweistel,Dreiph3r} is the name of the cipher under consideration.
All three ciphers are block ciphers that operate similarly. To encrypt a file, the file’s contents are read as a String and converted to a byte array using the method String.getBytes(). The byte array’s size is then increased to a multiple of the block size using a very simple padding scheme: the padding scheme inserts a single byte at the front of the byte array. This byte is intended to encode a non-negative integer n. The padding scheme then appends n bytes to the array, making the total size of the array m + n + 1, where m is the size of the original byte array. The padding scheme is implemented in the utils.Padder class. The byte array is then encrypted using the block cipher in ECB-mode. The generic encryption scheme is implemented in the BlockCipher class. The resulting byte array is encoded as a Base64-string string, which is finally written into the target file. Encoding and decoding is handled in the class ByteUtils.
Decryption reverses this process: the file containing the ciphertext is read, the Base64-encoded string is decoded into a byte array, the decryption function of the cipher is applied in ECB mode, the padding is reversed, the resulting byte array is converted to a string, and the string is written to the target file.
The file Main.java contains the main method of the program. When you run the program, it will encrypt the contents of the file files/Hello World.txt using the three ciphers, and decrypt the result again.
After running the program, the folder files should contain six more files – two for each cipher. One file should contain the encrypted contents of the file Hello World.txt. The other file’s contents should be identical to those of Hello World.txt. Before attempting the below problems, you should run the program to ensure it works correctly for you.
Problem 3.
Einstel is a block-cipher based on a Feistel network. It operates on 32-bit blocks and has a key size of 32 bits. It applies the Feistel iteration for 16 rounds using the kernel map that is described in the appendix. The key schedule is very simple: in even rounds it uses the 16 least significant bits of the key as the round key, in odd rounds it uses the 16 most significant bits of the key.
Give the decrypted contents of the file
files/Einstel/Unknown Ciphertext (Einstel).txt.
Give a brief summary of the method you have used to break the encryption.
Hint. To perform a known-plaintext attack, you will have to generate a plaintext-ciphertext pair from the text files. Remember that the plaintext byte-array is padded before encryption and that the ciphertext byte-array is Base64-encoded before being written to a file.
The methods encrypt and decrypt (available as overloads for byte arrays of size four and 4-byte ints) in FeistelNetwork32 perform side-effect free encryp-tion and decryption of a single 4-byte block. [20 marks]
Problem 4.
The block-cipher Zweistel is obtained by applying the Einstel cipher twice in sequence with two different keys. Give the decrypted contents of the file
files/Zweistel/Unknown Ciphertext (Zweistel).txt.
Give a brief summary of the method you have used.
Hint. You can perform a meet-in-the-middle attack. You could use Java’s HashMap to store ciphertext-key pairs. To avoid heap space allocation problems, I promise you that the 4-byte keys are smaller than 230 when interpreted as (signed) 32-bit integers.
The methods encrypt and decrypt (available as overloads for byte arrays of size four and 4-byte ints) in Zweistel perform side-effect free encryption and decryption of a single 4-byte block. [20 marks]
Problem 5.
The block-cipher Dreiph3r is not based on a Feistel network. It operates on 128 bit blocks and uses a 128 bit key.
For encryption, it performs the following operations to a 16-byte block of data for twelve rounds:
1. Perform a bit-wise XOR of the 16-byte key with the 16-byte block. The same key is used in every round.
2. Apply the AES S-box.
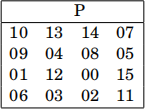
3. Apply the byte-wise permutation given by the following P-box:
More explicitly, the P-box represents the map
P(x0x1x2 ... x14x15) = x9x10x15 ... x3x4.
where x0,..., x15 are bytes.
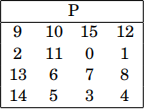
For decryption, the inverse of the AES-box and the inverse of the above P-box are used. Explicitly, the inverse of the P-box is given by

Give the decrypted contents of the file
files/Dreiph3r/Unknown Ciphertext (Dreiph3r).txt.
Give a brief summary of the method you have used.
Hint. The methods encrypt and decrypt in Dreiph3r perform side-effect free encryption and decryption of a single 16-byte block. [20 marks]
Appendix. The Kernel Map of the Einstel Cipher
The Einstel cipher performs the Feistel iteration Li+1 = Ri , Ri+1 = Li ⊕ f (Ri ,ki) using the kernel map
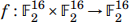
given by the following diagram:
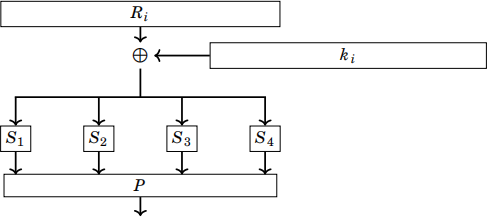
Where the S-boxes operate on 4 bit blocks, performing the following substitu-tions:
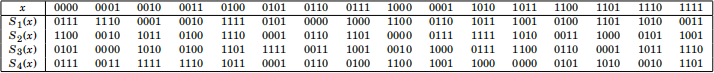
The above table is to be read as follows:
• On input 0000, the S-box S1 outputs 0111.
• On input 1000, the S-box S2 outputs 1000.
• On input 0101, the S-box S3 outputs 1111.
The P-box implements the following zero-indexed bit-wise permutation: