Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
MATH38032 Time Series Analysis
Examples sheet 1
1. (a) What is an iid sequence and what is a white noise?
(b) How is weak stationarity different from strict stationarity?
(c) What extra condition is required to conclude weak stationarity from strict stationarity?
(d) What extra condition is required to conclude strict stationarity from weak stationarity?
2. Use the definition of weak stationarity to show that {xt} given by xt = ε t+ θε t−1 , t ∈ Z
is weakly stationary and find its autocovariance and autocorrelation functions when {ε t} ~ WN(0,σ2) with σ > 0. [Hint: Show that the mean of xt is constant and the covariance of xt and xt+s is a function of s only.]
3. Let {xt} be a (weakly) stationary time series. If the time series {ε t} given by ε t = xt − axt−1 , t ∈ Z
is a white noise, where a =/ 0, show that the time series {et} given by
et = xt − a −1xt−1 , t ∈ Z
is also a white noise. [Hint: Write down the autocovariance functions of {ε t} and {et}, each in terms of that of {xt}, and compare them. A white noise has an autocovariance function that is proportional to the delta function.]
4. Find the autocovariance function of the (weakly) stationary time series {xt} given by
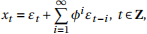
where |φ| < 1 and {ε t} ~ WN(0, σ2). [Hint: Use Theorem 2.]