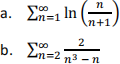Math 1C (MW)
Winter 2024
Problem Set 1: Sections 1.1, 1.2
(10 points)
Directions : Carefully write up your solutions to this problem set independently. Your solutions should not only demonstrate your understanding of the material, but also your ability to express the correct solution in writing in such a way that another person can make sense of it easily, including features such as clearly defined variables, well drawn and labeled figures, all steps shown in a clear and logical way, final answer clearly identified, etc. In grading this set, I will check the problem set for completeness, some of the problems for correctness, as well as how well the set is written up.
Problem Sets Submission Guidelines (from the Syllabus):
. Write out the problems neatly on separate paper, or on a blank tablet file. There is not enough room on the Problem Set PDF.
. You are encouraged to discuss the problems with your classmates, but you must write up your own solutions independently. Never copy anyone's work for any reason! Any instances of copying will lead to a grade of '0' on the affected Problem Set.
. Do the problems in order, showing all work neatly, clearly and completely.
. Label each problem clearly – use a highlighter to mark the number, or put a box around it so it's easy to find. You don’t need to write the question,just fully-worked out solutions.
. Don't squeeze a lot of work into a small amount of space. Leave some white space around your solutions for brief comments.
. Write your solutions out in full detail, as modeled in the textbook and in lectures. You should also draw well-labeled and appropriately scaled diagrams and graphs when relevant.
. Submit the Problem Set on paper in class. Alternatively, you may submit it as a single PDF document on Canvas. Use a scanning app such as Genius Scan. Your scanned copy must be legible and have correct orientation.
. Problem sets are due on Problem sets are due on Monday or Wednesday (see calendar) at the start of class. You can have a 24-hour extension with 10% penalty.
1. For each of the following sequences defined as a recurrence relations,
. List the first five terms of the sequence.
. Find a formula for the general term an in terms of n.
a. a1 = 2, an+1 = an + 2n for n ≥ 1
b. a1 = 2, an+1 = —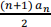 
for n ≥ 1
2. Find a formula for the general term an for the sequence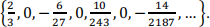 
Explain your logic briefly and check that your formula gives the correct answers.
3. Does the given sequence converge or diverge? If it converges, what does it converge to? Justify your answer carefully.
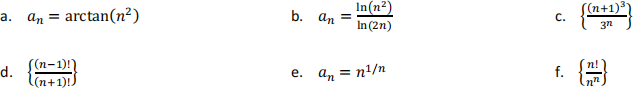
4. Consider the sequence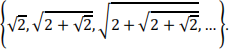 
a. Use mathematical induction to show that the given sequence is monotonically increasing.
b. Use mathematical induction to show that the given sequence is bounded above by 2.
c. Find the limit of the sequence.
5. Do the following series converge or diverge? Justify your answer logically. If series converges, find the sum. You may use any results obtained in class.
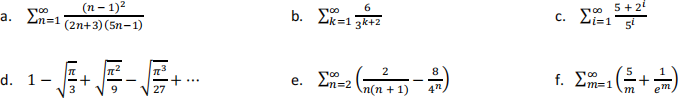
6. Suppose the nth partial sum of a series is given by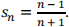 
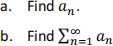
7. Express each of the following as telescoping series, find an expression for the nth partial sum sn, and find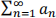 
if the series converges. Justify all steps carefully.
