CS 330: Introduction to Algorithms
Combinatoric Structures & Math Review
This is a compilation of facts, tricks and proof techniques that might come up with CS330. Use this problem set to test your skills and review the concepts that you are not comfortable with.
Tricks and facts
These are in no particular order.
1. xa · xb = xa+b and (xa )b = xab.
2. informal deinition: loga b = c ifac = b for a > 1. Because of this we get 2log2f(n) = f (n).
3. log x-· y = log x + logy and log y/x = log x — logy. From this what can you imply about log nc and
4. loga x = logba/logbx where a and b are constants. Because of this Θ(loga x) = Θ(logb x).
5. L’Hˆopital rule:
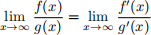
6. θ(nc1 ) < Θ(c2(n)) where c2 > 1.
7. Permutations: number of ways to put n diferent items in order. There are n! permutations.
8. Combinations:( k(n))= the number of ways we can choose a subset of k items out of n ( without repetition and so that the order of the k elements doesn’t matter).
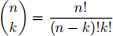
9.( k(n))=(nnk)
10. (a + b)n =(0(n))an +(1(n))an- 1 b +(2(n))an-2 b2 + . . . +(nn 1)ab + n — 1 +(n(n))a0 bn
11. 2n = Σ![]() i(n))= (1 + 1)n
i(n))= (1 + 1)n
12. tricks for O, Ω, Θ on slide.
Proofs
Combinatorics
Question 1. There are 10 copies of one book and one copy each of 10 other books. In how many ways can we select distinct backpacks of 10 books?
Question 2. A rook on a chessboard is said to put another chess piece under attack if they are in the same row or column. How many diferent ways are there to arrange 8 rooks on a chessboard (the usual 8 x 8 one) so that none are under attack?
Question 3. How many ways are there to arrange n children in a line if Alice and Bob always want to be next to each other? What is the answer if the order of the two does or doesn’t matter?
Question 4. How many ways are there to assign n children to two equally sized groups? (You may assume n is even) How many ways are there to assign them to two groups if the size of the two groups may be diferent?
Direct proof
Question 5. Prove the following using the deinition of the asymptotic notations.
1. ![]()
2. n2 = O(n3 )
3. n3 ![]() O(n2 )
O(n2 )
4. (1.3)pn ![]() Θ(2pn )
Θ(2pn )
5. pn = Ω(log n)
6. Suppose that f(x) and g(x) are two functions such that for some other function h(x), we have f(x) = O(h(x)) and g(x) = O(h(x)). Then f(x) + g(x) = O(h(x)).
Question 6. The sum of two even numbers if even. The sum of two odd numbers is even. The sum of an even and an odd number is odd.
Question 7. If n is even, then n2 is even. If n is odd then n2 is odd. If n is odd, then nk is odd.
Question 8. If 6n + 1 is divisible by 3 then so is 9n + 1. (Clearly the frst part of the statement is not true. Still we can prove that the second half follows if it were.)
Question 9. For integers x and y, if x2 + y2 is even, then so is x + y.
Question 10. Given that: 13 + 23 + . . . n3 = (1 + 2 + . . . + n)2 , prove that :k(n)=1 k3 = Θ(n4 )
Question 11. Show that for any two sets jAj + jBj = jA [ Bj + jA \ Bj .
Proof by contradiction
Being able to correctly state the negative of a statement is essential to this type of proof.
Question 12. Negate the following statements.
1. I own only black socks.
2. I don’t have any black socks.
3. I own black socks and white socks.
4. All of my socks are the same color.
5. None of my socks have holes.
6. Two of my socks have holes.
7. If spiders can swim, then all socks are black.
8. The CDS building is open to both faculty and students 24/7.
Question 13. Suppose a + b = 19. Then a ≥ 10 or b ≥ 10.
Question 14. For all integers if n3 + 5 is odd, then n is even.
Question 15. p2 is an irrational number. (A number is called rational if it can be written as the fraction of two integers.)
Question 16. Suppose n is a composite integer. Then n has at least one prime divisor that is pn.
Question 17. Prove that there are ininite many prime numbers. Hint: take the product of all primes and add 1 to it.
Induction
Question 18. Show that Σ![]() Σ k = 2/n(n+1) .
Σ k = 2/n(n+1) .
Question 19. Show that Σ![]() Σ k2 = 2/n(n+1) = 6/k(k+1)(2k+1) .
Σ k2 = 2/n(n+1) = 6/k(k+1)(2k+1) .
Question 20. .
1. Show that a set of size n has exactly 2n diferent subsets.
2. We know that 2n = Σk(n)=0(k(n)). Note that the sum is related to Question ??. Can you explain how these two relate intuitively? (This is not a proof by induction, just explanation in English.)
Question 21. You are laying out a pattern where you put square 1 * 1 tiles on the loor. The rule is that each new tile has to touch the entire edge of at least one of the tiles already laid. You can lay out any pattern with the tiles, the new tile can touch any of the existing ones, or multiple tiles, etc. Use induction on the number of squares to prove that the periphery of the tiles is always even.
Question 22. How many ways are there to go up a light of n stairs if with each step you can take either one or two stairs? How many ways if you can step 1, 2 or 3? How many if you can step any number between 1 to k? Write the corresponding recursive formula and prove by induction that it is correct.
Question 23. Let T be a rooted tree where each node can have 0, 1 or 2 children. We call a node a leaf if it has no children, and an inner node if it has exactly 2. Let ` be the number of leaves and i the number of inner nodes. Show that in any such tree the number of inner nodes is always one less than the leaves, thus i = ` - 1.
Question 24. Let T be a complete binary tree of height k. Show that it has exactly 2k - 1 vertices. Hint: use the left and right subtree of the root.
Question 25. Let Sn denote the number of n-bit strings that do not contain the pattern 00.
(a) Provide a base case and initial conditions for S1 and S2 .
(b) Write the recursive case for Si , i ≥ 3.