Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
MATH 5486-Spring 2024
Final Exam
Due: 3:30 PM CDT May 4th, 2024
1. The BVP y ′′ − q(x)y = r(x) with y(a) = y(b) = 0 is solved using the difference scheme
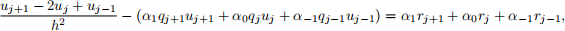
where j = 1, 2, · · · , N, rj = r(xj ), qj = q(xj ), u0 = uN+1 = 0, and h = (b − a)/(N + 1).
(a) (20 points) Assuming continuous higher order derivatives of y, q, and r, find α−1, α0, and α1, such that the truncation error is O(h 4 ). (Note: y (4) − [q(x)y] ′′ = r ′′(x))
(b) (10 points) Using your result from (a), give the linear system Ax = b (in component form) that must be solved to get the solution uj for j = 1, 2, · · · , N.
(c) (10 points) Prove: If q(x) ≥ Q > 0 and h is sufficiently small, then
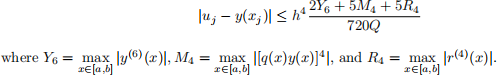
2. Consider the following 2-step method for solving the IVP ˙y = f(y), y(0) = y0.
yn+1 + a0yn + a1yn−1 = hbfn+1
(a) (10 points) How should a0, a1, and b be chosen to ensure the method is consistent?
(b) (10 points) How should a0, a1, and b be chosen to ensure the method is stable?
3. (40 points) The IVP ˙y = f(t, y), y(0) = y0 is integrated to get y(1) = y(0) + 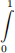 f(t, y(t))dt. Show that approximating the integral with the Gaussian quadrature formula
f(t, y(t))dt. Show that approximating the integral with the Gaussian quadrature formula 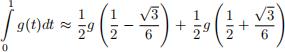 leads to the following Runge-Kutta method for solving the IVP.
leads to the following Runge-Kutta method for solving the IVP.
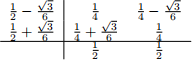
Remark: The Runge–Kutta methods take the form
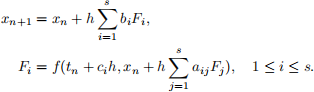
The coefficients of the method are collected together in the Butcher tableau as follows:
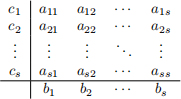
Hint: apply the Gaussian quadrature formula on the following integral