Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
AMME5520: Project Part 1
The following questions explore motion planning and linear control via the material from weeks 1-6. Submit a report through TurnItIn justifying the design decisions you have made and exploring their consequences. The report must be thorough but concise (feedback from your tutor will be valuable in achieving the right balance).
All matlab code must also be submitted through TurnItIn. While you are encouraged to discuss approaches with tutors and your fellow students, all code, analysis and submitted writing must be entirely your own work.
Other programming languages: for this assignment, werecommend that you use Matlab for all tasks. If you are very familiar with another language, e.g. Julia or Python, you may complete the assignment in this language but you should not expect help from the tutors in fixing any bugs. In Problem 1, equivalent rules about restrictions on libraries implementing graph search algorithms apply.
Problem Specification
You are in a team developing a robot waiter for the restaurant industry, and your job is to design the planning and control system for the robot. The hardware team have settled on a Segway-like two-wheel inverted pendulum type robot, which can move quickly between tables and take orders from customers.
A diagram of the robot is shown below, indicating some key variables.
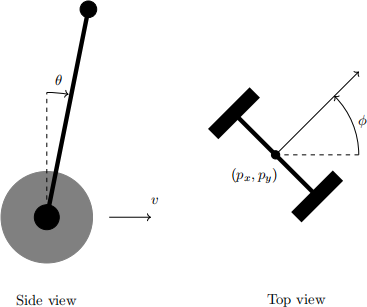
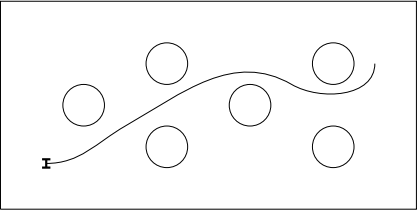
This robot is required to move around the restaurant, avoiding collisions with tables and maintaining balance and stability at all times. For this part of the project, assume the restaurant can be modelled as a open area with a number of circular obstacles representing tables, as illustrated below:
Checkpoints
The following checkpoints will be recorded, and may be taken into account in the marking of your report.
- Week 5: During your Week 5 tutorial, discuss your approach to Problem 1 with your tutor.
- Week 6: During your Week 6 tutorial, show your progress on Problem 1 and discuss your approach to Problem 2 with your tutor.
- Week 7: During your Week 7 tutorial, discuss your progress on Problems 2 and 3 with your tutor, as well as your draft report.
Problem 1 [30 marks]
Your task is to design and analyse a system for path planning from any given point to any other point in this map, by traversing obstacle-free regions in minimum time. The following workflow and discussion points for your report are suggested:
1. (10 marks) Build a probabilistic roadmap of the restaurant floor, with tables of fixed radious randomly placed around the floor. In building your PRM, be sure to test edges for collision (how?).
2. (10 marks) Implement Dijkstra’s algorithm to find shortest paths between points on this map, and test it with a variety of initial and final locations.
3. (10 marks) Propose a heuristic and implement A⋆ . Is your heuristic ad- missable and consistent? What happens if you use a heuristic which isn’t? Compare to Dijkstra’s algorithm in terms of the final result and compu- tational effort for a variety of start and end goals.
For this question you may use only basic Matlab functions and the functions described above from the Image Processing toolbox. In particular, you may not use any functions or toolboxes that implement graph-search algorithms such as Dijkstra or A⋆ . You may, however, use the Matlab Grader problem from Week 3 as inspiration.
Basic Matlab functions are considered to be those found in the documen- tation (type doc in the command window) under the following headings: Lan- guage fundamentals, Graphics, Programming Scripts and Functions, and under Mathematics the following subheadings: Elementary Math, and Linear Algebra.
Problem 2 [30 marks]
The state of the robot consists of body angle θ and angular rate θ(˙), forward velocity of the base v, and the 2D position px , py and orientation ϕ relative to the restaurant floor.

Each wheel has a motor that can apply a torque. For simplicity we assume that one control inputs, u1 , represents the sum total torque applied between the wheels and the body, and a second input u2 represents the differential velocity of the two wheels.
The physical parameters are the wheel radius ρ, and the combined mass M and moment of inertia of the wheels JM , the mass of the body m, its moment of inertia Jp , and the distance l between the body centre of mass and the centre of the wheels.
The dynamics of the robot can be derived as
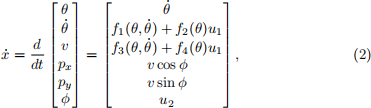
where
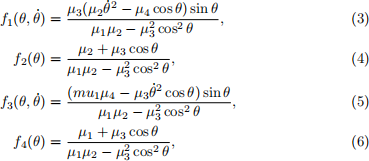
and
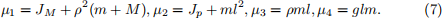
The following tasks are suggested:
1. (5 marks) Choose reasonable parameters for ρ,M,JM ,m, Jp and l for your robot. You will use these parameters in future parts of Project parts 1 & 2.
2. (10 marks) Calculate the operating points (state variables) of the robot for standing still and moving forwards at 1m/s. I.e. find the angle θ such that θ(˙) = v = 0 is possible, and another angle θ so that θ(˙) = 0 and v = 1 are possible for some u1 .
3. (10 marks) Notice that dynamics of the angle/speed variables (θ, θ(˙),v, u1 ) do not depend on px , py ,ϕ . Consider this subsystem and linearise the dynamics about the operating points calculated in the previous part, re- sulting in systems of the form
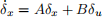
where δx ,δu represent deviations from the operating point.
4. (15 marks) For each operating point, assuming all states are measurable, design an LQR controller and simulate it with the original nonlinear dy- namics.
- Examine the effect of different choices of weighting matrices, and justify your design.
- Examine the response to different initial conditions.
- Examine the similarity/differences between the linearised and non- linear models.
Problem 3 [30 marks]
In this problem you will combine your solutions from Problems 1 & 2. The objective is to design a complete control system that guides the robot from one location to another while avoiding collisions.
1. (15 points) Considering all state variables (i.e. θ, θ(˙),v, px , py ,ψ) design a system that follows a straight line path from one end to another.
- You may choose to do this as a single controller, or by building an outer loop around your angle/speed controller from the previous problem. Justify your design decisions in your report.
- Simulate your controller from a variety of initial conditions, and dis- cuss its response.
- Simulate with the nonlinear dynamics, and check for stability and collision avoidance.
Report Quality [10 marks]
In addition to the marks above for technical work, 10 marks will be allocated for the presentation and structure of your report and any associated code.
It is expected that your report is well-written, clearly formatted, design decisions are well justified, and the results are concisely but thoroughly analysed, and that any Matlab code is well-structured, legible, and properly commented. Any figures should be legible and clear.
You may provide short code snippets within the report to illustrate ideas, and you must also upload all code