PX390. Assignment 4: Wave function
November 29, 2023
The aim of this assignment is to find eigenfunctions of the wave equation
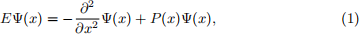
where E is the eigenvalue (energy), P(x) is a given function and Ψ(x) is a real valued function defined on the domain x ∈ [xL, xR].
Boundary conditions at points xL and xR are given by:
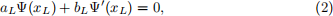
on the left side of the domain and one on the right
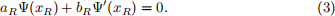
Coefficients aL, bL, aR, bR are input parameters. Note that all the parameters and functions are continuous and real-valued.
To solve this problem, the code should formulate the eigenvalue equation as a matrix equation
where Ψ is a numerical representation of the wavefunction and M is a matrix representing the RHS of the wave equation. You should choose an initial guess for Ψ, Ψ0 (to make this easier to test, make sure this random guess is the same for every run of the code). We then iterate the following equation:
to produce an increasingly accurate guess for the eigenfunction. E0 is an input parameter and a correct code will converge towards the eigenvector nearest E0 for large i.
You are required to use the LAPACK library to invert matrices, so the com-piler flags are different this time. This library is installed on the lab computers and on vonneumann. We will not provide any support for installing these li-braries on your own computers, it might be quicker just to log in to vonneumann to test your program. In order to compile your program (here, named prog4.c) on vonneumann you need to execute the following commands:
1. module purge
2. module load intel impi imkl
3. gcc prog4.c -lmkl -liomp5 -lm
You also need to add
#include
in your source code. As before, you should test your code with simple test cases. We will, again, be marking it mostly based on how well it reproduces certain tests.
As before, you should test your code with simple testcases. I will, again, be marking it mostly based on how well it reproduces certain tests.
1 Suggestions on getting started
❼ The easiest way to call LAPACK is to use the matrix example codes band utility.c as a framework for setting the values of the matrix at par-ticular locations and solving the inverse problem.
❼ It may be helpful to recall some known analytic solutions of the given wave equation from quantum mechanics. Also, note that the eigenfunctions of M are also eigenfunctions of (M − E) −1 . You should use this to test your results against known analytic solutions.
❼ The boundary conditions require an extension of the ideas shown in the lectures for second order derivatives. You can extend the domain to in-clude ’ghost points’ outside the domain and use Taylor expansion to apply the boundary conditions at the grid points within the domain of your nu-merical solution.
2 Specification:
The input and output grid should have N grid points, which include the end of the domain, that is, the x domain runs from xL = x0 to xR = xN−1.
Input:
The input parameters will be read from a file called ‘input.txt’ and must be given in the order specified below (their types are specified in parenthesis)
1. xL (double), left x boundary of domain.
2. xR (double), right x boundary of domain.
3. N (long int), number of grid points
4. aL (double), first left boundary condition coefficient.
5. aR (double), first right boundary condition coefficient.
6. bL (double), second left boundary condition coefficient.
7. bR (double), second right boundary condition coefficient.
8. E0 (double), guess for initial eigenvalue.
9. I (long int), number of iterations.
You may assume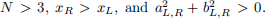 
Note that the example input file provided with this specificcation does not necessarily give a valid set of inputs for a specific problem. It is sufficient to use scanf to read in these parameters and simply test that the reads were successful. While we do not specifically forbidding the use of other ways of reading input, roughly 50% of students attempting a more complicated input scheme got it wrong in the past.
The function P(x) will be given at the N grid points as a column of double precision numbers in a file called ‘potential.txt’. There are example input files and output file on the assignment page.
Output:
For diagnostic purposes you will output Ψ at each step of the iteration. The code should stop when it has performed I iterations and thus found ΨI . The output file name must be ‘output.txt’. It must contain three columns i, x, Ψi(x), where i ∈ [0, I] is the iteration number, x is a grid point and Ψi is the eigenfunction approximation at step i.