Practice Problems 1
Econ 702, Spring 2024
Question 1
Suppose a household solves the following two-period consumption-savings problem with taxes
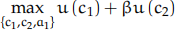
subject to
c1 + a1 = y1 − T1 + a0
and
c2 = y2 − T2 + (1 + r) a1
with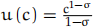 
and where y1 and y2 are their incomes in periods 1 and 2, T1 and T2 are the taxes paid in periods 1 and 2 respectively and a0 is the initial wealth of the household.
1. Solve for the household’s choice of c1, c2 and a1 in closed form. In other words solve for these objects in terms of the parameters of the model
2. How does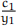 
depend on y2? What would happen if the households became more optimistic about the future?
3. How does 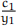depend on a0? Interpret your result.
4. How does 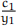depend on β? Interpret your result.
5. Suppose y2 = T1 = T2 = 0. Compute 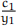. How does the answer depend on σ?
Interpret your answer.
Question 2
Consider a T-period economy in which production takes place according the following technology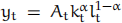 
where kt is the capital stock and lt, labor. Assume that a fraction δ of the capital stock depreciates each period. Suppose that this economy is pop-ulated with a large number of identical households who are endowed with one unit of time and who have preferences given by
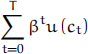
Assume that output can either be consumed or invested and used as capital the following period.
1. Write down the resource constraint of this economy
2. Write down the Social Planner’s problem.
3. Characterize the solution to the Planner’s problem.
4. Now suppose that there exists a large number of firms who rent capital and hire labor to operate the production technology. The firms are owned by households. Let µt be the rental rate on capital and wt, the wage rate. Write down and characterize the firms problem
5. Suppose that households can consume and save at rate rt. Write down and charac-terize the households problem
6. Define a competitive equilibrium (CE)
7. How do the allocations associated with a CE compare with those from the social planner’s problem?
Question 3
Consider the following two-period model. Households have preferences
u (c1) − v (l1) + β (u (c2) − v (l2))
where ct is consumption and lt is the labor choice of the household. Here v (l1) represents the disutility of working and v is an increasing and convex function. The household is endowed with one unit of time. Suppose the household can supply labor and receive a wage rate wt as well as save in in period 1.
1. Write down the households problem. What conditions characterize this problem?
Interpret these conditions
2. Suppose that there exists a large number of firms who rent capital and hire labor to operate the production technology. The firms are owned by households. Let µt be the rental rate on capital and wt, the wage rate. Write down and characterize the firms problem
3. Define a competitive equilibrium (CE)
4. Set up and characterize the Social Planner’s problem
5. Does the solution of the social planner’s problem and the equilibrium coincide?