Coursework 2: MATH 3018/6141 - Numerical methods
Due: 12:00 Monday 8th January 2024
In this coursework you are to implement the numerical algorithms that are outlined and described below. The assessment is based on
. correct implementation of the algorithms – 6 marks
. correct use of the algorithms in tests and figures to illustrate algorithms and tests – 8 marks
. documentation of code – 1 mark
The deadline is noon, Monday 8th January 2024 (week 12). For late submissions there is a penalty of 10% of the total marks for the assignment per day after the assign- ment is due, for up to 5 days. No marks will be obtained for submissions that are later than 5 days.
Your work must be submitted electronically via Blackboard using the Python tem- plate file provided on Blackboard. Only the Python file needed to produce the output specified in the tasks below is required.
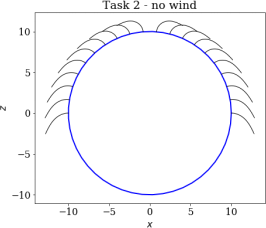
Figure 1: Locations of 20 hairs in the x,z plane under the force of gravity alone. The boundary value problem for each hair is solved by fixing the location where the hair meets the head.
1 Modelling hair
A major use of numerical methods is in the creation of computer graphics in films, games, and other media. The generation of “realistic” animations of, for example, smoke, or water, or explosions, are typical problems. One case that remains difficult is the simulation of hair, particularly under external forces such as wind and rain. Here you will be asked to simulate human hair in 2-dimensions.
2 Model
The first reasonable model of human hair used the beam equation applied to each hair individually. This coursework follows that model. The model we use here makes a number of simplifying assumptions:
1. The human head is a sphere with radius 10 cm.
2. Each hair meets the head normal to the sphere.
3. The forces acting on each hair are gravity (in the -z direction) and a constant wind (in the +x direction).
We want to contruct the location of each hair. We will use the parameter s, which measures arclength along the hair, with s = 0 being the point where the hair meets the head and s = L being the point at the free end of the hair. Here we assume that L = 4 cm is the constant hair length.
The model works separately for each hair. It uses a mixture of coordinate systems. The location of the hair will be displayed in the (x, z) coordinate system. The location
of the hair will depend on the value of the independent variables along its length. The independent variable s takes the value s = L at the free end of the hair and, at the location where the hair meets the head, takes the values = 0. The spatial position that the hair joins the head (at s = 0) is given by

Here θ0 is a coordinate on the head that describes the latitude (angle away from hori- zontal).
In contrast the angle θ(s) describe the local orientation (in space) of a given hair. The fact that the hair comes out of the head at right angles is given by the boundary conditions

The hair then bends under the influence of gravity and the wind force. Bending is described by the orientation θ(s) changing with s, as we go along the length of the hair. A completely rigid hair would have constant θ(s). The simplified bending model leads to a system of an ODE for each individual hair, which reads
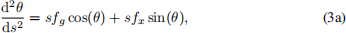
Here fg is a parameter describing the force from gravity relative to the bending stiffness of the hair. An appropriate value for human hair is fg = 0.1 cm-3 and we use this here.
The other parameter, fx , describes the force from the wind relative to the bending stiffness of the hair. In addition, the hair can move freely at its end (at s = L), which leads to the boundary condition

We can determine θ(s), by solving the BVP defined in equation (3) with the two sets of boundary conditions found in equations (2) and (4). Once the angle θ(s) has been determined, the (x, z) coordinates of the hair can be found by solving the ODEs

with initial conditions given by the location at which the hair emerges from the head via equation (1).
3 Task
1. Write a function that, given L,R, fx , fg , and a list of values of θ0 which specify where the hairs meet the head, returns the (x, z) coordinates of the hairs.
2. Fix fx = 0 (no force due to the wind). Recall that fg = 0.1 throughout. Compute and plot the location of 20 different hairs, with L = 4, which meet the head with position (determined by equation (1)) with values of θ0 evenly spaced on the interval [0, π]. Plot the locations in the (x, z) plane.
3. Repeat the previous task with fx = 0.1.
3.1 Summary and assessment criteria
You should submit the code electronically using the template provided, as noted above.
The primary assessment criteria will be a general code that solves the hair-modelling problem. In top-level code comments the reasons for the choice of algorithm should be clearly given, stating the (dis)advantages of this and alternative methods.
The secondary assessment criteria will be the correct implementation of the tests and production of the plots. The clarity of the output (such as plots or results printed to the command window) is important.
Your functions and scripts must be well documented with appropriate internal com-ments describing inputs, outputs, what the function does and how it does it. The code should also be well structured to make it easy to follow. Code efficiency is not impor-tant unless the algorithm takes an exceptional amount of time to run.
The original paper that uses a “physical” approach to hair modelling is by Anjyo et al. from 1992. A survey of hair modelling approaches is given by Bartails et al. (2006). The particular model used here is a generalisation of Howison’s book on Practical Ap-plied Mathematics. For a broader range of modelling techniques applied to computer graphics, Ron Fedkiw’s webpage is a good place to start.