Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due

COS 433/533 Problem Set 1

Collaboration Policy. You are encouraged to collaborate with other students on the problems.

Please list all collaborators in your submission along with all other resources consulted. The use of large language models is not permitted. Please write up all solutions on your own.

1 COS 433 Problems

Problem 1: Statistical Distance (Probability Review)

Let X0 and X1 denote random variables over a finite outcome set X . Define the statistical distance between X0 and X1 as

That is, ∆(D0, D1) is the largest distinguishing advantage that can be attained by some “test” event T ⊂ X applied to X0 and X1. Prove that
Problem 2: Tail Inequalities (Probability Review)

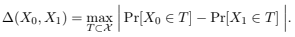
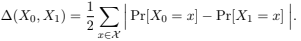
In the following problem, you may assume for simplicity that all of the relevant random variables take values in some finite outcome space.

(a) Markov’s Inequality. Let X be a non-negative real random variable. Prove that for any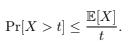

(b) Chebyshev’s Inequality. Let X be a real random variable with variance σ². Prove that for any t > 0,

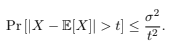
(Hint: Apply Markov’s Inequality to a function of X)

(c) Averaging Independent Random Variables. Let X1, . . . , Xn be a collection of n indepen- dent random variables. Suppose that for some constant σ, we are guaranteed that Var[Xi] ≤ σ² for every i.

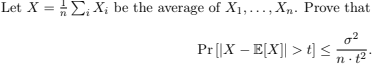
Can you state a relaxation of the independence assumption on X1, . . . , Xn that still allows us to deduce the inequality?

Problem 3: Shannon’s Lower Bound

Let (Enc, Dec) denote an encryption scheme for n-bit messages (M = {0, 1}

(a) Consider a randomized encryption scheme satisfying perfect security, but with a relaxed correctness property: for all messages m, it is guaranteed that
Prove that in this relaxed setting, we still must have λ ≥ (1 − O(δ))n.
Optional Bonus: Suppose that δ = .1. Can you show that λ ≥ n?

(b) Consider a randomized encryption scheme satisfying perfect correctness, but with a relaxed security property. For any message m, let Cm denote the distribution

Our relaxed security property is that for all pairs of messages (m0, m1), the two distributions (Cm0 , Cm1 ) have statistical distance at most ε.

Prove that in this relaxed setting, we still must have λ ≥ (1 − O(ε))n.

Problem 4: Distributing the Nuclear Codes
The President is in possession of the launch codes of a nuclear weapon; the codes are represented as a uniformly random binary string s ← {0, 1}
l of length l. The President has a cabinet of n
Secretaries that she mostly trusts, but not completely.
In the event that the President is incapacitated or killed by a foreign adversary, she would like to ensure that her cabinet remains in possession of the nuclear codes. However, she does not want to give each Secretary a copy of the codes – too risky.
(a) Devise a scheme in which the President can ensure that:
• If all n Secretaries pool their information together, they can determine s.
• If strictly fewer than n of the Secretaries pool their information together, their probability of guessing s is 2−l.
Moreover, in your scheme, each Secretary should only need to store l bits of information. Prove that your scheme satisfies all of these properties.
Hint in footnote below.1
(b) The President fears that the scheme from part (a) still risks losing the codes – what if the president and a secretary are taken out?
Devise a scheme in which the President can ensure that:
• If any two of Secretaries pool their information together, they can determine s.
• Any individual Secretary can only guess s with probability 2−l.
In your scheme, each Secretary should only need to store ≤ l · n bits of information.
(c) Optional Bonus: Suppose that n < 2
l. Can you solve part (b) so that each Secretary only needs to store l bits of information?
Hint in footnote below.2
2 COS 533 Problems
You may want to review the COS 433 problems to check your understanding. However, this is optional, and you should not turn them in unless stated below.
Problem 1: Do COS 433 Problem 3.
Problem 2: A stronger tail inequality
In COS 433 problem (2c), we deduced a tail inequality for sums (or averages) of independent random variables by using Chebyshev’s inequality. In this problem, we will prove a much stronger tail inequality by (implicitly) using higher moments of that random variable.
(a) Hoeffding’s Lemma Let X be a c-bounded mean-zero random variable, i.e. E[X] = 0 and |X|≤ c with probability 1. Prove that for any λ > 0,
(b) Chernoff-Hoeffding Inequality. Let X1, · · · , Xn be i.i.d. (independent, identically dis- tributed) mean-zero random variables, with |Xi|≤ c. Prove that for any t > 0,

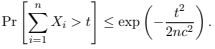
Hint in footnote below.3

This implies that the average 1 is highly concentrated around its expectation, to within error O ̃(c/√ n), with overwhelming probability.

The Chernoff bound is used frequently in cryptography and cryptanalysis, and more generally throughout theoretical computer science.