Instructions:
· Type your response in a separate “word doc” named LastName_FirstName.doc
· You must upload your R script. I do not accept “.Rmd” format, so please convert everything into raw R file.
· Do not use the forecast, quantmod, tseries or the strucchange package, AIC or BIC or arima function or basically, any packages that were not covered in the lecture. You will not receive any score for responses associated with these packages. If you are not sure, please consult me first before your submission.
· Upload 2 files (Word doc and 1 R files) on Blackboard
This project consists of two parts:
· Part 1: Predicting Stock Returns.
· Part 2: Forecasting models for the unemployment rate.
· Part 3: Cointegration Investigation.
Part 1: Predicting Stock Returns
a. Use the Autoregressive Distributed Lag Models to estimate the following over the 1990 January–2023 June sample period. For the unemployment rate variable, you only need to show the output from (t-6) and (t-1), whichever is applicable. For each block, you need to show the coefficients, heteroskedastic standard error and the associated p-value.
|
Dependent variable: Excess returns on the CRSP value-weighted index
|
|||
|
|
(1) |
|
(2) |
|
Specification |
ADL(1,6,1,1) |
|
ADL(2,12,2,2) |
|
Estimation Period |
1990:M1–2023:M6 |
|
1990:M1–2023:M6 |
|
Regressors |
|
|
|
|
Excess Ret(t-1) |
|
|
|
|
Std. Error |
|
|
|
|
p-value |
|
|
|
|
|
|
|
|
|
Excess Ret(t-2) |
|
|
|
|
Std. Error |
|
|
|
|
p-value |
|
|
|
|
|
|
|
|
|
Unemployment Rate(t-6) |
|
|
|
|
Std. Error |
|
|
|
|
p-value |
|
|
|
|
|
|
|
|
|
Unemployment Rate(t-12) |
|
|
|
|
Std. Error |
|
|
|
|
p-value |
|
|
|
|
|
|
|
|
|
10-Year CMT Rate(t-1) |
|
|
|
|
Std. Error |
|
|
|
|
p-value |
|
|
|
|
|
|
|
|
|
10-Year CMT Rate(t-2) |
|
|
|
|
Std. Error |
|
|
|
|
p-value |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Std. Error |
|
|
|
|
p-value |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Std. Error |
|
|
|
|
p-value |
|
|
|
|
|
|
|
|
|
Intercept |
|
|
|
|
Std. Error |
|
|
|
|
p-value |
|
|
|
|
|
|
|
|
|
Adj R^2 |
|
|
|
|
|
|
|
|
|
F-statistic |
|
|
|
|
p-value |
|
|
|
|
Obs = |
|
|
|
b. Are these results consistent with the theory of efficient capital markets?
c. Which specific data point of the result assert your above statement?
d. Incorporate one additional economic variable from (https://fred.stlouisfed.org) with any additional lag of your choice. Did it improve the R2?
e. Construct pseudo out-of-sample forecasts of excess returns with rolling 10-year window and the regression specifications below that begin in 2000 January (1st month with 10-year available historical data).
Zero Forecast: the sample RMSFEs of always forecasting excess returns to be zero.
Constant Forecast: (in which the recursively estimated forecasting model includes only an intercept
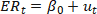
In R, this is equivalent to running lm(ER ~ 1). Note that you still need to use the rolling window to calculate the “Constant Forecast”. This means the constant forecast should change every month from 2000 January to 2023 June, because in each month, a new set of 10-year monthly data is incorporated into the regression.
ADL (2,12,2,2) specification as in (a):
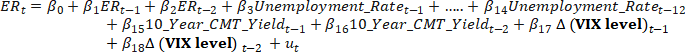
|
Model |
RMSFE |
|
Zero Forecast |
|
|
Constant Forecast |
|
|
ADL (2,12,2,2) |
|
f. Does the ADL (2,12,2,2) provide better forecasts than the zero or constant models?
Part 2
Forecasting models for unemployment rate
In this exercise you will construct forecasting models for the unemployment rate, based on UNRATE.
(i) Plot a line chart of the monthly unemployment rate. Based on the plot, do you think that unemployment has a stochastic trend? Explain.
(ii) Compute the first twelve autocorrelations of
a. Monthly unemployment rate (Unemploy)
b. Change of monthly unemployment rate (ΔUnemploy)
(iii) Plot the value of ΔUnemploy. The plot should look “choppy” or “jagged.” Explain why this behavior is consistent with the second autocorrelation that you computed in (ii. b.)
(iv) Compute Run an OLS regression of Unemployt on Unemployt-1. Does knowing the unemployment this month help predict the unemployment next month? Explain using your result and data.
(v) Estimate an AR(2) model for Unemploy. Is the AR(2) model better than an AR(1) model? Explain.
(vi) Estimate an AR(p) model for Unemploy. What lag length is chosen by BIC? What lag length is chosen by AIC?
(vii) Use the AR(2) model to predict the level of monthly employment in 2024 February.
(viii) Use the ADF test for the regression in Equation (15.32) with two lags of ΔUnemploy to test for a stochastic trend in Unemploy. Does the unemployment rate have a unit root?
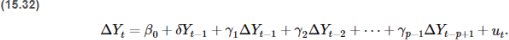
(ix) Is the ADF test based on Equation (15.32) preferred to the test based on Equation (15.33) for testing for stochastic trend in Unemploy? Explain using your data and result.
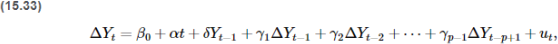
(x) In (viii) you used two lags of ΔUnemploy. Should you use more lags? Fewer lags? Explain with specific test and data.
(xi) Use the QLR test with 15% trimming to test the stability of the coefficients in the AR(2) model for Unemploy. (You must not use the strucchange package. You must demonstrate that you understand how the QLR test is structured as illustrated in the class) Is the AR(2) model stable? Explain.
(xii)
(i) Using the AR(2) model for Unemploy with a sample period that begins in 1970:M01, compute pseudo out-of-sample forecasts for the unemployment rate beginning in 2005:M12 and going through 2024:M1.
(ii) Are the pseudo out-of-sample forecasts biased (ie. Non-zero mean)?
(iii) How large is the RMSFE of the pseudo out-of-sample forecasts? Is this consistent with the AR(2) model for Unemploy estimated over the 1970:M01–2024:M1 sample period?
(iv) Identify the month when there was an outliner in the unemployment data. What happened to that period?
Part 3
Investigation of Cointegration Within the Stock Market
From the Time Series Lectures, you learned that when two data series are linearly dependent (with stationary residual), the series are said to be cointegrated. Any exogenous forces that change this relationship are considered temporary and the series that drift beyond its usually pattern will presume to autocorrect its path to re-establish the preexisting linear relationship. This mechanism was historically exploited by investment analyst as a quantitative trading strategy. In this exercise, you will choose two stocks or financial instruments that you believe to be closely “related” and use the Engle-Granger Augmented Dickey-Fuller test to determine whether it is worthwhile to construct a pair-trading strategy.
1) Pick two U.S. Stocks or financial instrument that you believe to be cointegrated and want to examine their feasibility for pair-trading. State the rationale AND elaborate of why you choose these two stocks. Here are some considerations or ideas on informing this decision:
a. Choose two companies that compete in the same market where they earn revenue from the same segment/group of end-users.
b. From the list of S&P 500 constituents, choose companies in the same GICS sector.
c. Plot the return charts. Have they moved in the same “pattern” historically?
2) Download the historical monthly stock return (10-Year) from Yahoo Finance.
3) When conducting the Engle-Granger Augmented Dickey-Fuller test, you should assume that you do not know the cointegrating coefficient between the stocks’ return. Therefore, you will need to perform a linear regression and estimate the residual.
In your write-up, please explain if two stock return series are cointegrated, how you will devise a pair-trading strategy to profit from a pattern drift? You must illustrate in drawing of how the strategy will profit. Sorry, you cannot just copy from the output of ChatGPT; you need to demonstrate that you understand the concept of cointegration.