CSCI-GA.1170-004 Fundamental Algorithms
Problem Set 1
January 24, 2024
Due: 5 pm on Tuesday, January 30
Problem 1-1 (Asymptotic Comparisons) 10 points
For each of the following pairs of functions f(n) and g(n), state whether f is O(g); whether f is o(g); whether f is Θ(g); whether f is Ω(g); and whether f is ω(g). (More than one of these can be true for a single pair!)
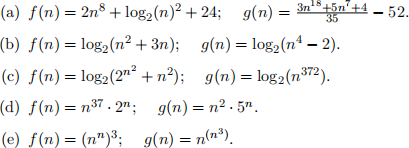
Problem 1-2 (Order of Growth) 12 points
(a) (8 points) For each of the following functions f(n), find a “canonical” function g(n) such that f(n) = Θ(g(n)). For example, 3200n + 2n 2 log24(n 2 ) = Θ(n 2 log24 n). Briefly justify your answers (and I mean briefly).

(b) (4 points) Based on your answers in part (a), sort the resulting “canonical” (not original) functions in asymptotically increasing order.
Problem 1-3 (Matching Numbers) 16+3 points
You are given a set of n points x1, ..., xn and a set of n segments [a1, b1]...[an, bn] on a line, where xi , ai , bi are all integers. We want to output k1, k2..., kn, where ki is the number of segments that contain xi . More formally, let X[1, . . . , n] be the array storing the points. Moreover, let I[1, . . . , n] denote an array storing the segments such that each entry I[i] stores two values I[i].lef t and I[i].right. We want to write an algorithm that computes K[1, . . . , n] with K[i] being the number of segments containing the point X[i]. In the following, assume that all the points, starting points, and endpoints are distinct.
(a) (1 point) Assume you solve the problem using a naive algorithm which iterates through all point-segment pairs, what is the running time?
In the following, we develop a more clever algorithm. To this end, we first create an auxiliary array C[1, . . . , 3n] that stores the points as well as start and end points of the intervals. Each entry C[j] stores three values: C[j].value that is an integer, C[j].type that is either of the literals “left”, “right”, or “point”, and a value C[j].pointer that stores an index between 1 and n into one of the original arrays.
(b) (3 points) Write the pseudocode of a procedure GenerateC(X, I, n) that fills the above described array C based on the arrays X and I.
(c) (4 points) Assume now that the above described array C has been generated and then sorted according to the value field, i.e., such that C[i].value < C[i + 1].value for all i from 1 to 3n − 1. Write a procedure ComputeK(C, n) which computes the array K[1, . . . , n] in time Θ(n) by iterating over the array C once.
(d) (2 points) Assume you use the best sorting algorithm you know from the lecture so far, what is the overall running time when combining the solutions from parts (b) and (c) to solve the overall problem?
(e) (4 points) Argue the correctness of part (c) using a suitable loop invariant.
(f) (2 points) Now assume that collisions between points and start or endpoints of the intervals can happen, as well as collisions between multiple intervals. For instance, we could have that X[i] = I[j].lef t, that I[i].lef t = I[j].right, or that I[i].lef t = I[j].lef t for some i and j. Show that if we do not make any assumptions on how the sorting algorithm breaks ties, that then our algorithm is incorrect. To this end, provide an example input X and I and a sorted corresponding C such that your algorithm from part (c) produces the wrong result.
(g) (Extra Credit)(3 points) Generalize your algorithm from part (b) in such a way that the combined algorithm, with unmodified part (c), correctly works even in the presence of collisions. The format of the array C should remain unchanged and we still do not make any assumption on how the sorting algorithm breaks ties. (Hint: You may consider tweaking the values stored in C[i].value.)