Macro-Econometrics
Homework Assignment #9 (150 points)
This assignment is based on the data in the Excel worksheet HW_Data_Period_9.xlsx, which is found on the course website. The data set contains 100 observations for three simulated data series – X, Z and Y. These data were generated by the instructor based on a model where all three variables are non-stationary and co-integrated. By construction, the three data series have two common trends and one co-integrating relationship. However, in this exercise, you will pretend that you are uncertain about these properties.
(a). Plot each of the three series. The data do not appear to be stationary. Based on what you see in the plots, what sort of non-stationary model(s) would you consider as possible candidates – trend stationary, unit root with drift, or unit root without drift?
(b). Conduct an augmented Dickey-Fuller test (as below) for each variable, using lag lengths p of 0 (no lags) and 4 (four lags). Report your results for the γs in a short table. What do you conclude?
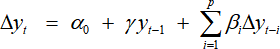
Now, impose the null of a unit root and test for the significance of the constant. What are your results? Finally, re-test for a unit root but do not include a constant. What are your results? Do they match with your assessments in (a)?
(c). Estimate the following long-run cointegrating relationships (estimated separately):
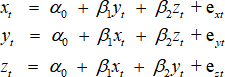
Report your results for the βs in a table, along with the t-statistics. Why can’t you conduct inference using these t-statistics?
(d). Using the 3 sets of residuals from part (c), test for stationarity (you do not need to report your results). Why can’t we use the usual DF tables to make inferences about stationarity? Which table is appropriate for finding the correct critical values? Using a 5% critical value, what is the correct critical value? What do you conclude?
(e). Now, estimate an error correction model using the error-term from the 1st equation in part (c) and 1 lag of Δx, Δy, and Δz. The easiest way to do this is to estimate a VAR model, and enter the equilibrium errors as “exogenous variables”. Remember to lag them! Present your results for the adjustment coefficients in a concise table with coefficient estimates and t-statistics. Which error-correction coefficients are statistically different from zero? What critical value did you use? Are there any pitfalls in using that critical value?
(f) . Are the estimated error-correction coefficients consistent with LR convergence to your estimated cointegration vectors in (c)? Why or why not? Please be specific in your answer by carefully matching up each adjustment coefficients with the appropriate coefficient in the LR relationship that you estimated in the first equation of part (c).