MTH6105 – Algorithmic Graph Theory
Spring 2024
Assessed Coursework 1
1. Let the degree sequence of a graph G be the sequence of length |V (G)| that contains the degrees of the vertices of G in non-increasing order.
(a) For each of the following sequences, either draw a simple graph whose de-gree sequence is equal to that sequence, or explain why such a graph does not exist: (i) (4, 4, 4, 2, 2), (ii) (4, 2, 2, 1, 1), (iii) (3, 3, 3, 2, 1), (iv) (4, 3, 3, 2, 1), (v) (2, 2, 2, 1, 1).
(b) Consider a simple graph with 9 vertices, such that the degree of each vertex is either 5 or 6. Prove that there are at least 5 vertices of degree 6 or at least 6 vertices of degree 5.
2. Let G be a graph and e ∈ E(G). Let H be the graph with V (H) = V (G) and E(H) = E(G)\ {e}. Then e is a bridge of G if H has a greater number of connected components than G.
(a) Let G be the simple graph with V (G) = {u, v, w, x, y, z} and E(G) = {uy, vx, vz, wx, xz}. For each e ∈ E(G), state whether e is a bridge of G. Justify your answer.
(b) Assume that G is connected and that e is a bridge of G with endpoints u and v. Show that H has exactly two connected components H1 and H2 with u ∈ V (H1) and v ∈ V (H2). To this end, you may want to consider an arbitrary vertex w ∈ V (G) and use a u−w-path in G to construct a u−w-path or a v−w-path in H.
(c) Show that e is a bridge of G if and only if it is not contained in a cycle of G.
3. (a) Determine the Pr¨ufer code of the following tree.
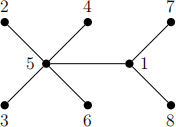
(b) Draw the trees with Pr¨ufer codes (i) (3, 2, 3, 2, 3), (ii) (5, 5, 5, 5, 5), and (iii) (6, 5, 4, 3, 2).