CS 3800-Online
Spring 2024
Homework 1
(due Friday, January 19)
Instructions: This homework is to be submitted on GradeScope as a single pdf (not in parts) by 11:59 pm on the due date. You may either type your solutions in a word processor and print to a pdf, or write them by hand and submit a scanned copy. Do write and submit your answers as if they were a professional report. There will be point deductions if the submission isn’t neat (is disordered, difficult to read, scanned upside down, etc....).
Begin by reviewing your class notes, the slides, and the textbook. Then do the exercises below.
Show your work. An unjustified answer may receive little or no credit.
Read: 0.1, 0.2 (for Tuesday) and 0.3, 0.4 (for Friday)
1. [6 Points] For the Tseitin word problem discussed in class, are the words in the following pairs equivalent? Prove your answers (either by showing a sequence of substitutions or by proving that none exists).
(a) cadbcedb and caccaebd
(b) bccdbc and cbbdcc
(c) aecdab and cade
2. [7 Points] Consider the following word problem, similar to Tseitin’s but with only
❼ the two letters in {a,b}
❼ the single substitution a = aa
(a) Are the strings abaabbab and aaababbaab equivalent? Prove your answer.
(b) Is there an algorithm to decide this word problem, that is, an algorithm that on input any two strings always correctly outputs whether they are equivalent or not? Prove your answer by describing such an algorithm or showing that none exists.
3. [8 Points] Tseitin used the 5 symbols a,b,c,d,e and 7 substitutions to construct a word problem undecidable by algorithms. Show that the number of symbols can be reduced from 5 symbols to 2 symbols (such as 0 and 1) while preserving undecidability.
4. [8 Points] Which of the following conditional statements are true and why? (For each statement, determine its form among T → T , T → F , F → T , F → F).
(a) If February has 30 days, then 7 is an odd number.
(b) If January has 31 days, then 7 is an even number.
(c) If 7 is an odd number, then February does not have 30 days.
(d) If 7 is an even number, then January has exactly 28 days.
5. [4 Points] Let x be a positive real number. Use a proof by contrapositive to show that if x is irrational (i.e., not a rational1 number), then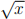 
is also irrational.
(a) Write the contrapositive of the statement “if x is irrational, then 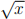is irrational”.
(b) Prove this contrapositive.
6. [4 Points] Write a full CNF with variables p,q,T that has the truth table
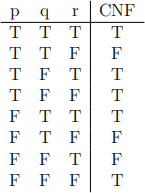
7. [6 Points] In this problem, the domain is the set Z of integers and we consider the state- ment φ:
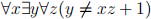
(a) Use De Morgan’s laws to write the negation – φ, simplifying to the point that no ‘–’ symbol occurs anywhere in your statement (you may, however, use binary relation symbols such as ‘=’, ‘≠’, ‘<’, and ‘>’).
(b) Which of the two statements φ and – φ is true? Carefully explain your answer.
8. [7 Points] For this problem, the domain is the set of Northeastern students. Consider the following two predicates
Charlie(x) meaning “ Charlie knows x ”
CS(x) meaning “ x is a CS student ”
Using only variables, logic symbols (selected from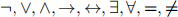 
), and the pred- icates Charlie and CS, formulate the statements:
(a) Charlie doesn’t know every CS student.
(b) The only students known to Charlie are CS students.
(c) Charlie knows at least two students.