BUSN9970 Prescriptive Analytics for Decision Making
Individual Written Assessment on Mathematical Modelling and Computation
Instructions
This coursework consists of two independent problems (see below). For each problem, you need to:
a) Present the mathematical model (e.g. decision variables, objective function and constraints, and any key assumptions).
b) Build an OPL model (the data must be read from a .dat file).
c) Run the OPL model and record the optimal objective function value and solution of each problem instance.
d) Write a concise problem summary.
As part of each problem summary, please include the following:
• A copy of your OPL code. For this, you just need to copy your code (model and data files) from the CPLEX Studio IDE and paste it at the end of the document (e.g. a Word file) containing your summary.
• The main results for the given problem instance (e.g. the optimal objective value, decision variables, etc.)
• Your analysis and interpretation of the results.
Keep your report concise and within the word count limit of 2000 words.
Remember good OPL programming practice: make your models general by not hard coding in data.
You need to submit electronic copies of the problem summaries and OPL files in a single .zip file via Moodle by 12:00 (noon) Wednesday 17 January 2024. This assessment is worth 30% of your overall mark for BUSN9970.
Plagiarism Policy
Projects should be done individually. The submitted work must be completed solely by yourself. Do not share or discuss your work with other students. Copied code is quite easy to spot so do not be tempted to work with anyone else. Anyone found violating the plagiarism policy will receive a mark of 0 for the assessment in addition to any University disciplinary action. This applies equally to the one receiving and to the one giving out his/her work.
Problem 1: Shortest Path Problem (40 marks)
Jasper Ridge Reserve is a popular nature reserve that has been set aside for a limited amount of sightseeing and hiking. Cars are not allowed into the reserve, but there is a narrow, widening road system for off-road vehicles (e.g. jeeps and quad bikes) driven by park rangers. A network representation of the road system is shown below, where location O is the entrance to the reserve. The other letters designate the locations of ranger stations and other scenic spots. The numbers along each arc give the distance (in miles) of intervening road sections.
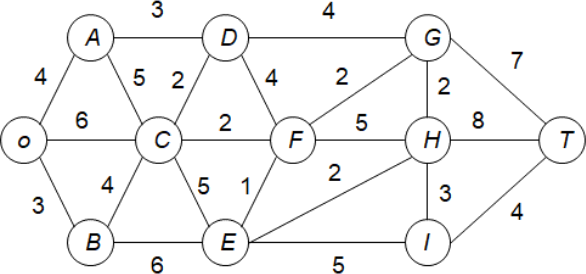
The reserve contains a scenic wonder at station T. A small number of large jeeps are used to transport sightseers from the reserve entrance to station T and back. The reserve manager would like to determine the shortest route from the reserve entrance to station T. [Hint: Use the LP formulation of the shortest path problem covered in class].
Problem 2: Warehouse Location (60 marks)
An online retail company in the US is planning to open warehouses in potential locations shown on the map below. The distance (in miles) between each pair of locations and the demand of each location are given in tables below.
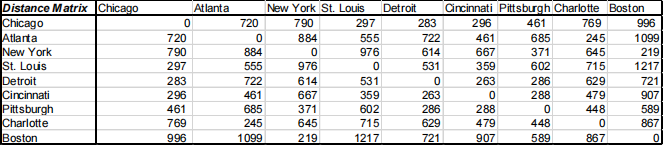
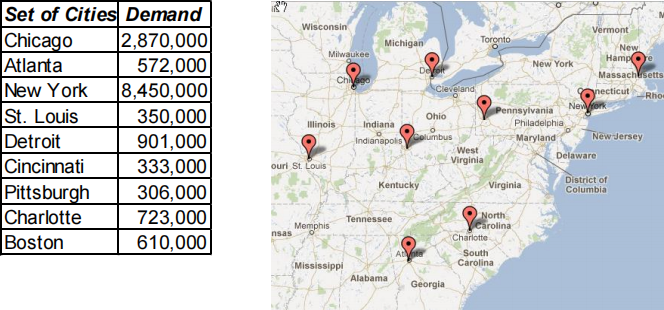
(a) Formulate a mathematical model that minimises total weighted distance between demand points and their nearest warehouse, with weight being the demand of each location. Assume the company open only p warehouses due to budgetary limitations. Explain the objective function and constraints. Solve the problem for p = 3 and compare the results with p = 4 and p = 5. (30 marks)
(b) Now imagine that the company would like to ensure that no demand location is more than 500 miles away (maximum distance) from a warehouse and wishes to maximise total demand that can be covered within a 200 mile distance (high service distance). Update the model developed for part (a) accordingly and explain the objective function and constraints. Solve the model for p = 3, p = 4, and p = 5 and for high service distances of 200, 250, and 300 miles. (15 marks)
(c) Analyse/interpret the results from each part and compare the solutions based on metrics such as total weighted distance, maximum number of customers within high service distance, total number of warehouses opened, maximum distance from a warehouse to a customer location. (15 marks)