CPT108: Data Structures and Algorithms
Semester 2, 2023-24
Assignment 1
Problems
Problem 1. Given 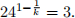 Find the value of 2k. (3 marks)
Find the value of 2k. (3 marks)
Problem 2. You are given the coeficients a0 ,..., an of a polynomial [Cormen 2-3 (a,b)]
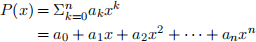
and you want to evaluate this polynomial for a given value of x. Horner’s rule says to evaluate the polynomial according to this parenthesization:
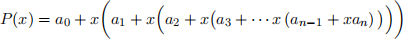
The procedure HORNER implements Horner’s rule to evaluate P(x), given the coeficients a0 ,..., an in an array A[0 : n] and the value of x
HORNER(A, n, x)
1 p = 0
2 for i = n downto 0
3 p = A[i] + x · p
4 return p
(a) In terms of θ-notation,what is the running time of this procedure? (2 marks)
(b) Write pseudocode to implement the naive polynomial-evaluation algorithm that computes each of the polynomial from scratch. What is the running time of this algorithm? How does it compare with HORNER? (6 marks)
Problem 3. The following recurrence often arises in divide-and-conquer algorithms, where the processes of dividing and combining involves sorting.
where nisa power of 2. Prove that T (n) = Θ(nlg2 n). (4 marks)
Problem 4. Suppose that for inputs of size n on a particular computer, insertion sort runs in 8n2 steps and merge sort runs in 64nlgn steps. For which values of n does insertion sort beat merge sort? (Hint: You may need to test different values of n to indthe correct answer.) (4 marks) [Cormen 1.2-2]
Problem 5.
Here is an array often integers:
|
5 |
3 |
8 |
9 |
1 |
7 |
0 |
2 |
6 |
4 |
Draw this array after the FIRST iteration of the large loop in an insertion sort
(sorting from smallest to largest). (5 marks)
Problem 6. Here is an array which has just been partitioned by theirst step of quick sort:
|
3 |
0 |
2 |
4 |
5 |
8 |
7 |
6 |
9 |
Which of these elements could be the pivot? (There maybe more than one possi-bility!) (2 marks)
Problem 7. Banks often record transaction on an account in order of the times of the transactions, but many people like to receive their bank statements with checks listed in order by check number. People usually write checks in order by check number, and merchants usually cash them with reasonable dispatch. The problem of converting time-of-transaction ordering to check-number ordering is therefore the problem of sorting almost-sorted input. Explain persuasively why the procedure INSERTION- SORT might tend to beat the procedure QUICKSORT on this problem. (5 marks) [Cormen 7.2-4]
Problem 8. Here is an array of eight integers:
|
5 |
3 |
8 |
9 |
1 |
7 |
0 |
2 |
Draw this array after the TWO recursive calls of merge sort are completed, and before the inal merge step has occurred. (5 marks)
Problem 9. Consider the following recursive program.
1 private int foo(int x, int n) {
2 if (n == 0) return 1;
3
4 if (n % 2 == 1) {
5 y = foo(x, (n - 1) / 2);
6 return x * y * y;
7 }
8 else {
9 y = foo(x, n / 2);
10 return y * y;
11 }
12 }
(a) What is the output for foo(2,7)? (2 marks)
(b) What does the program do? (2 marks)
(c) Analyze the worst-case running time of the program using Big-Oh (O), assuming that nisa power of 2. (Show all steps.) (4 marks)
Problem 10.
(a) Does the following array represent amin-heap (Yes/No) ?
|
3 |
6 |
7 |
23 |
41 |
19 |
27 |
29 |
(b) Given the following max-heap of size 10:
|
45 |
37 |
29 |
20 |
18 |
27 |
13 |
4 |
8 |
14 |
Delete the maximum from the max-heap and give the resulting max heap in a form of an array. (3 marks)