Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
FIN2020 Homework 5
1.The CAPM and the APT
Consider an economy in which the random return r;on each individual asset i is determined by the market model
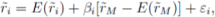
where,as we discussed in class,E(ri)is the expected return on asset i,fm is the return on the market portfolio,β;reflects the covariance between the return on asset i and the return on the market portfolio,and e;is an idiosyncratic,firm-specific component.Assume,as Stephen Ross did when developing the arbitrage pricing theory (APT),that there are enough individual assets for investors to form many well-diversified portfolios and that investors act to eliminate all arbitrage opportunities that may arise across all well-diversified portfolios.
a.Write down the equation,implied by the APT,that links the expected return E(rw)on each well-diversified portfolio to the risk-free rate rf,the expected return E(rx)on the market portfolio,and the portfolio's beta βw
b.Explain briefly(one or two sentences is all that it should take)how the equation you wrote down to answer part(a),above,differs from the capital asset pricing model's (CAPM's)security market line.
c.Suppose you find a well-diversified portfolio with beta βw that has an expected return that is higher than the expected return given in your answer to part (a),above.In that case,you can buy that portfolio,and sell short a portfolio of equal value that
allocates the share w to the market portfolio and the remaining share to 1-w to a risk-free asset.What value of w will make this trading strategy free of risk,self-financing,but profitable for sure?
2.A Two-Factor APT
Consider an economy in which the random return f;on each individual asset i is given by
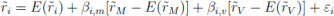
where,as we discussed in class,E(ri)equals the expected return on asset i,fm is the random return on the market portfolio,fv is the random return on a“value”portfolio that takes a long position in shares of stock issued by smaller,overlooked companies or companies with high book-to-market values and a corresponding short position is shares of stock issued by larger,more popular companies or companies with low book-to-market values, ei is an idiosyncratic,firm-specific component,and βi,m and βi,are the “factor loadings” that measure the extent to which the return on asset i is correlated with the return on the market and value portfolios.Assume,as Stephen Ross did when developing the arbitrage pricing theory(APT),that there are enough individual assets for investors to form many well-diversified portfolios and that investors act to eliminate all arbitrage opportunities that may arise across all well-diversified portfolios.
a.Consider,first,a well-diversified portfolio that has βwm =βu =0.Write down the equation,implied by the APT,that links the expected return. on this portfolio to the return rr on a portfolio of risk-free assets.
b.Consider,next,two more well-diversified portfolios.portfolio two with βu,m =1 and βw,v=0 and portfolio three with βum =0 and βw=1.Write down the equations, implied by this version of the APT,that link the expected returns and on each of these two portfolios to rf,E(rm),and E(rv).
c.Suppose you find a fourth well-diversified portfolio that has non-zero values of both βwm and βu,and that has expected return
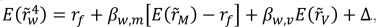
where △<0 is a negative number.Explain briefly how you could use this portfolio, together with the first three from parts(a)and(b),above,in a trading strategy that involves no risk,requires no money down,but yields a future profit for sure.