MAT A22
Homework # 5 –
Winter 2024
Homework Guidelines
This homework was released on Fri. Feb. 9th 14:00 (EST). It is due on Fri. Feb. 16th 17:00 (EST).
We encourage you to talk to your TAs during tutorial, attend office hours, and ask professors for help with this assignment. You may use the textbook without citing it as a reference, however all other books and internet sources must be cited. Please submit your original work via Crowdmark.
The version of this homework on Crowdmark is the only official version of the assignment. This PDF is provided for your refer-ence. Please check the version on Crowdmark before uploading your solutions.
For this assignment, Question 3 must be typed up in LATEX.
Readings
❼ ➜2.1 Linear Transformations
❼ ➜2.2 Linear Transformations between Finite-Dimensional Vec-tor Spaces
Problems
Q1. Let L(V, W) be the set of linear transformations from V to W. Prove that the set L(V, W) forms a vector space using the following operators. Let S, T ∈ L(V, W) and c ∈ F
(S ⊞ T)(v) = S(v) ⊕ T(v)
(c ⊡ T)(v) = c ⊙ T(v)
where ⊕ is the vector addition operator from W and ⊙ is the scalar multiplications operators from W. (Remember to show closed un-der addition and multiplication.) Suppose, V and W are both finite dimensional, determine the dimension of L(V, W).
Q2. For each of the following, determine if T : V → W is a linear transformation. Provide an appropriate proof if true and a counter example if false.
(a) V = R2 and W = R 2 . T(x1, x2) = (x1 − x2, 3x2 + 2x1)
(b) V = R2 and W = R 2 . T(x1, x2) = (x1x2, x2 − x1)
(c) V = R2 and W = R 2 . T(x1, x2) = (1 − x1, x2)
(d) V = R2 and W = R 3 . T(x1, x2) = (0, x1 − x2, x1 + x2)
Q3. (******This question is to be typed up in LATEX******)
Let V = R 3 and W = R 2 . Let T ∈ L(V, W) such that
T(1, 1, 0) = (2, 1), T(1, 0, 1) = (1, 1) and T(0, 1, 1) = (−1, 2).
Let v1 = (1, 1, 0), v2 = (1, 0, 1) and v3 = (0, 1, 1).
(a) Express x ∈ V as a linear combination of v1, v2, v3.
(b) Compute T(x).
Q4. Let V = R 3 and W = R 2 . Let T ∈ L(V, W) such that
T(1, 1, 1) = (2, 1), T(1, 2, 1) = (−1, 1) and T(3, 1, 1) = (−1, 2).
Let v1 = (1, 1, 1), v2 = (1, 2, 1) and v3 = (3, 1, 1).
(a) Express x ∈ V as a linear combination of v1, v2, v3.
(b) Compute T(x).
In questions 5 and 6 you will explore the standard inner product a little more. Recall the definition of the standard inner product.
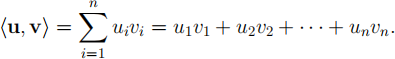
Q5. Prove that the standard inner product satisfies the following prop-erties.
(a) ⟨⃗u, ⃗v⟩ = ⟨⃗v, ⃗u⟩
(b) ⟨⃗u, ⃗v1 + ⃗v2⟩ = ⟨⃗u, ⃗v1⟩ + ⟨⃗u, ⃗v2⟩
(c) ⟨⃗u, a⃗v⟩ = a⟨⃗v, ⃗u⟩
(d) ⟨⃗u, ⃗u⟩ ⩾ 0, with equality if ⃗u = 0.
Q6. Let V = R n . Suppose W is a subset of V . The set W⊥ is the set of vectors perpendicular to W.
W⊥ = {x ∈ R n : ⟨x, v⟩ = 0, for all v ∈ W}
Prove that W⊥ is a subspace of V . (You may reference Q5a, Q5b, Q5c, or Q5d as justification if needed)
Q7. Consider a = (x1, x2, x3) ∈ R3 , b = (y1, y2, y3) ∈ R3 . The cross product of a and b, denoted a×b, is given by the following equation
a × b = (x2y3 − x3y2, x3y1 − x1y3, x1y2 − x2y1)
Prove the following:
(a) a × b ∈ (span({a, b}))⊥
(b) If a and b are collinear, then a × b = 0.
(c) What is the dimension of (span({a, b}))⊥ if
1. a and b are collinear?
2. a and b are not collinear?
Q8. Let V be the set of continuous real valued functions. Define the appropriate vector space W for each situation and prove that the following well know functions are linear transformations.
(a) The derivative operator.
(b) The definite integration operator Int(f) =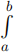 
f(x)dx.
(c) The definite integration operator Int(f) =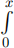 
f(t)dt.