Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
MATH 237 Online Calculus 3 for Honours Mathematics
Spring 2024
Mini-midterm 2
Due date: 11:30pm, June 28 2024
1.(30 points) Partial derivatives.
(i) (15 points) Determine the differentiability of the following function at p0, 0q:
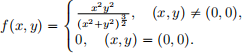
(ii) (15 points) Suppose z = f(r) and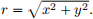 
Then use the chain rule to show that
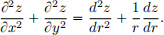
2.(30 points) Suppose g(x,y, z) = 3ln(x + eyz ).
(i) (10 points) Find the gradient of g.
(ii) (20 points) Calculate the directional derivative of at (0, 1, 0) in the direction from the point (0, 1, 0) to the point (5, 3, 3).
3.(30 points) Suppose f(x,y) = ln (—2sin2 x + 4cos2 y).
(i) (15 points) Find the linearization at (0, 0), L(0 ,0)(x,y).
(ii) (15 points) Find the second order Taylor polynomial at (0, 0), P2 , (0 ,0)(x,y).
4.(10 points) Miscellaneous problems.
(i) (5 points) Suppose φ(u) is a one-variable function such that for any u ∈ @, Iφ(u)I ≤ u2 . Determine the differentiability of f(x,y) = φ(IxyI) at (0, 0).
(ii) (5 points) Suppose the second order partial derivatives off(x,y) exist. Moreover, we assume f(x,y) > 0 for any x,y. Then show that f(x,y) = g(x)h(y) for some one-variable function g,h if and only if
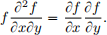
(Hint: Consider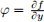 
and try to calculate 
)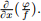