Subject of Economics
Degree of Degree of Asset Pricing and Investment MSc, Financial Economics
MSc, Quantitative Finance MSc
Degree Exam
Economic Fundamentals and Financial Markets, ECON5005
Friday, 6 th May 2022, 9:15 – Saturday, 7 th May 2022, 9:15
Exam duration: 2 hours
Section A
Answer one question from this section.
1 More on empirical tests of stochastic equilibrium model but using UK data. Download the attached spreadsheets.
(a) UK stock market returns
(b) returns to low-risk UK bonds
(c) UK consumption data
(d) VIX implied volatility index
Note that the data are all in terms of annual rates of return (stock market, bonds and implied volatility) or annual rates of growth (consumption). Where the raw data was in percentage terms I have added a column which divides the percentage figures by 100.
Carry out the following tasks filling in the results on the spreadsheet and also documenting your procedure and results in your answer sheet. Upload the spreadsheet calculations as well as your answer sheet.
1.1 Calculate the risk aversion coefficient using the consumption growth data. [25 points]
1.2 Calculate the Sharpe ratio divided by the variance method discussed in slide 3 (estimate the volatility directly using the data in the spread-sheets and the Excel variance calculator). [25 points]
1.3 Repeat the above exercise but use the average implied volatility from the VIX spreadsheet. [25 points]
1.4 Briefly compare and contrast the results. [25 points]
2 Deterministic optimal growth model. Let

A representative individual solves

subject to
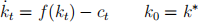
2.1 Write the appropriate Hamiltonian [10 points]
2.2 State the solution for consumption as a function of the costate vari-able. [10 points]
2.3 State the equation for the costate variable. [10 points]
2.4 State the steady-state capital. [15 points]
2.5 State the steady-state interest rate. [15 points]
2.6 State the flow of profit in the steady state. [15 points]
2.7 State the price of an equity share in the representative firm in the steady state. [15 points]
2.8 State the equation for the interest rate along the growth path (not just at the steady state), assuming that the initial capital is k0. [10 points]
Section B
Answer one question from this section.
3 An individual solves an optimal portfolio problem as follows:

where his wealth evolves according to

Notice that ct does not appear in the utility function or on the right hand side of the wealth equation.
3.1 Write down the consolidated wealth process dWt . [10 points]
3.2 Write down the HJB equation. [10 points]
3.3 State the optimality condition for the portfolio holding α. [10 points]
3.4 Conjecture a form for V , and also state the derivatives Vw and Vww for the conjectured form. Your conjecture might have one or more constants; because this is an exam I do not expect you to solve for the constant(s)—just carry them forward to this and later questions in abstract form. [10 points]
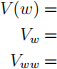
3.5 State the solution for the optimal holding of the risky asset α using the conjectured form (leaving the unknown constant(s) undetermined for now). [15 points]
3.6 Substitute the conjectured form of the value function V into the HJB equation, along with the actual utility function and simplify (but again you do not need to solve for the abstract constant(s)). [15 points]
3.7 Write down the Wt process under the assumption that α = 1. Note that no measure change has been imposed. [15 points]
3.8 In the lectures we discovered that the state price ξt is equal to the first derivative of the value function Vw; set ξt ≡ Vw. Using Ito’s lemma, state the stochastic process for dξt , under the assumption that α = 1. [Hint: Because Vw is a function of Wt use the dWt process from your answer to the previous subquestion. Note again that no measure change has been imposed.] [15 points]
4 Measure change/state price
Let

Let
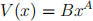
The “physical” measure is P. Consider a measure change to Q, such that the St process has drift r under Q.
4.1 State the derivatives Vx, Vxx. [20 points]
4.2 State the V process under the P measure using Ito’s lemma. [20 points]
4.3 State the X process under the Q measure. [Note: Unlike the sim-ilar tutorial problem, nothing has been stated about the Sharpe ratio for the X process.] [20 points]
4.4 Now make an additional assumption: that the Sharpe ratio for the Vt process is the same as the Sharpe ratio for the St process. [Note that this is different from the tutorial assignment.] Verify that de−rtVt is a martingale under the Q measure by applying Ito’s lemma. [20 points]
4.5 Continuing with the Sharpe ratio assumption, find the β of the Vt. [20 points]