MATH6153W1
SEMESTER 1 EXAMINATION 2016/17
Statistical Theory and Linear Models
1. Suppose that X1 , . . . , Xm+n are a random sample from the standard normal
distribution where m and n are known positive integers. Suppose k < m + n - 1 is also a positive integer.
(a) [6 marks] Using as many as necessary of X1 , . . . , Xm+n, write down a new
random variable, which has the χ2 distribution with k degrees of freedom. Using the moment generating function, or otherwise, prove this result when k = 1.
(b) [3 marks] Using as many as necessary of X1 , . . . , Xm+n, write down a new random variable which follows the standard t distribution with k degrees of freedom.
(c) [4 marks] Using X1 , . . . , Xm+n, write down a new random variable which
follows the standard F distribution with m and n degrees of freedom respectively for the numerator and the denominator. Hence state a relationship between the t distribution with k degrees of freedom and an equivalent F distribution.
(d) [12 marks] Suppose that X and Y are independently normally distributed with
mean 0 and variance σx(2) = 2(1 + ρ) and σy(2) = 2(1 - ρ), respectively where
-1 < ρ < 1 is a known parameter.
(i) [4 marks] Write down, fX,Y (x, y), the joint pdf of X and Y.
(ii) [8 marks] Consider the transformation X and Y to U and V where

Find the joint pdf of U and V , fU,V (u, v) by applying the transformation method. Name the joint distribution of U and V. In general, are U and V independent? State what happens when ρ = 0.
2. Suppose that X1 , . . . , Xn are a random sample from the random variable X having the pdf:

(a) [7 marks] Show that Y = X2 follows the exponential distribution. Obtain the parameter of this distribution and hence write down the value of E(Y). Assuming E(X) = 1/2 √ πθ, find the variance of X .
(b) [5 marks] Show that the expected Fisher information for θ is I(θ) = .
(c) [7 marks] Find the maximum likelihood estimator (mle) of θ. Is themle unbiased and does its variance achieve the Cram![]() r-Rao lower bound?
r-Rao lower bound?
(d) [6 marks] By equating E(X) and X(-) = ![]() Σ
Σ![]() Xi, find a method of moments
Xi, find a method of moments
estimator of θ. Is this estimator unbiased? [Hint: Use the results stated and
obtained in part (a)].
3. As in Question number 2, assume that X1 , . . . , Xn are a random sample from the random variable X having the pdf:
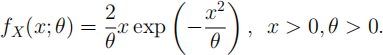
Let x1 , . . . , xn denote the random observations. You may assume the distribution theory stated or asked to be proved in Question number 2.
(a) [4 marks] State the Neyman-Pearson Lemma for testing H0: θ = θ0 against H1: θ = θ1 .
(b) [7 marks] Consider the problem of testing H0: θ = θ0 against H1: θ = θ1 where θ 1 > θ0. Show that the critical region of the most powerful test for testing H0
against H1 can be expressed as
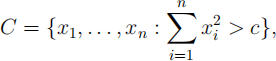
for some c > 0. Hence conclude that this testis also the uniformly most powerful test for testing H0: θ = θ0 against Ha: θ > θ0 .
(c) [6 marks] Show that Z = ![]() Σ
Σ![]() Xi(2) follows the χ2 distribution with 2n degrees of freedom. You may assume that the sum of independent χ2 random variables also is a χ2 random variable.
Xi(2) follows the χ2 distribution with 2n degrees of freedom. You may assume that the sum of independent χ2 random variables also is a χ2 random variable.
(d) [3 marks] Show that c = θ0/2 k for the level α uniformly most powerful test, where k is such that P (χ2(2)n > k) = α .
(e) [5 marks] Using the distribution of Z, construct a 100(1 - α)% confidence interval for θ .
4. (a) [13 marks] The following linear model is proposed for random variables Y1 , Y2 , Y3:

where x1 = — 1, x2 = 0, x3 = 1 and the Ei , i = 1, 2, 3 are independent and normally distributed with zero mean and common variance σ2 .
(i) [6 marks] Write down the design matrix and hence evaluate the least squares estimators for α and β .
(ii) [7 marks] Show that the random variables Y2 + Y3 and Y1 — Y2 + Y3 are independently normally distributed. Find their means and variances. Hence
show that the statistic
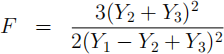
is distributed as the standard F random variable under the null hypothesis
H0 : α = 0. What are the two degrees of freedom for the above F?
(b) [12 marks] A random variable Y has an inverse gamma distribution, IG(m, β) if it has the pdf

A particular measuring device has normally distributed error with mean zero and unknown variance σ2. In an experiment to estimate σ2 , n independent evaluations, denoted by x1 , . . . , xn, of this error are obtained.
Suppose that the prior distribution for σ2 is IG(m, β) for some given values of m and β .
(i) [6 marks] Show that the posterior distribution is also IG(m* , β * ) and derive expressions for m* and β* .
(ii) [6 marks] Show that the predictive distribution for the error, Xn+1, of a further observation made by this device has pdf
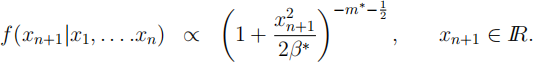
What is the name of this distribution? State the values of its parameters.