Assignment 2: ECON-UA 266 - Intro to Econometrics
Fall 2023
Question 1 [5 points]
Show that  .
.
Question 2 [15 points]
Let X and Y have joint pdf: PX,Y (x, y) =  , where x = 1, 2, 3 and y = 0, 1
, where x = 1, 2, 3 and y = 0, 1
a. [5 points] Find the Covariance and correlation of X and Y (write the formula and then find the covariance and coefficient of correlation)
b. [5 points] Find E[Y|X] (again write the formula first)
c. [5 points] Calculate directly E[E[Y|X]] and hence show that it is equal to E[Y]. This is known as the law of iterated expectation.
Question 3 [10 points]
In class, we introduce two different concepts to study the relationship between X and Y . The first object was the Conditional Expectation Function (CEF), and the second object was the univariate linear regression model (LRM). Although the CEF is not always linear, when it is linear, then the LRM is the CEF. One special case where the CEF is linear is when X takes one of two values as follows:
Consider E[Y|X] where X is a dummy variable that equals one with probability p and is zero otherwise. Prove that the CEF and the regression of Y on X are the same in this case. Do this by showing that for Bernoulli X:
α = E[Y ] − βE[X] = E[Y |X = 0]
β = Cov(X, Y )/V ar(X) = (E[Y |X = 1] − E[Y |X = 0])
Question 4 (Wooldridge Chapter 2 question 5) [15 points]
In the linear consumption function
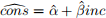
where the (estimated) marginal propensity to consume (MPC) out of income is simply the slope, while the average propensity to consume (APC) is 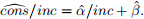
Using observations for 100 families on annual income and consumption (both measured in dollars), the following equation is obtained:
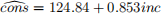
a. [5 points] Interpret the intercept in this equation, and comment on its sign and magnitude.
b. [5 points] What is the predicted consumption when family income is $30, 000?
c. [5 points] With inc on the x-axis, draw a graph of the estimated MPC and APC
Question 5 [15 points]
A college bookseller makes calls at the offices of professors and forms the impression that professors are more likely to be away from their offices on Friday than any other working day. A review of the records of calls, one-fifth of which are on Fridays, indicates that for 16% of Friday calls, the professor is away from the office, while this occurs for only 12% of calls on every other working day. Define the random variables as follows: X is equal to one if the call is made on Friday and zero if the call is made on Monday to Thursday and Y is equal to one if the professor is away from the office and zero if the professor is in the office.
a. [5 points] Find the joint probability function for X and Y .
b. [5 points] Find the conditional probability function for Y given X = 1 and X = 0.
c. [5 points] Find E[Y|X]
Data Question 1 [20 points]
Download data from the 2010 Census at a geographic level of the state or lower [the TA will tell you how to access the dataset]. Choose data to generate two variables that will make up a SLRM but one variable CANNOT be median household income. Your data set must have AT LEAST 30 observations.
1. [5 points] Describe your data; include the period of analysis, the number of observations, the location, and the geographic level of the data.
2. [5 points] Describe your variables. This will include the definitions of these variables and the summary statistics (mean and standard deviation). DO NOT include the R output at part of your homework; rather write a sentence that indicates the value of these statistics.
3. [5 points] Write down the population LRM that is based on these two variables. Explain why this is an economically interesting relationship (i.e. what economic theory/reasoning indicates that the independent variable, X, causes the dependent variable, Y ?). What is the predicted sign of the slope coefficient in your regression?
4. [5 points] Run a regression using these two variables and interpret the slope parameter estimate from this regression. Include the regression table [hint: you can use stargazer or summary] as part of your homework.
Data Question 2 [15 points]
Download data from 2016 CPS (the TA will help you find the data during recitation – look at the March CPS) which contains observations on weekly earnings, sex, race, age and education for respondents aged 25-64.
a. [5 points] Plot the weekly earnings of individuals against the number of years of education.
b. [5 points] Take the logarithm of the weekly earnings and plot the new variable against the number of years of education. Do you see a difference in the relationship between the two variables? Does it make sense to take the logarithm if we are interested in a linear model?
c. [5 points] Get the summary statistics of the your data.