ECON 300 - Intermediate Microeconomics
Winter 2024
Problem Set 1
Due: January 14th, 2024
1. (25 points) Consider the following 8 bundles of goods x and y
A = (8, 4) B = (5, 6)
C = (5, 9) D = (10, 3)
E = (1, 4) F = (6, 5)
G = (2, 8) H = (7, 8)
(a) (8 points) Come up with an example of a utility function that will produce the following order of preference for the bundles:
H ≻ C ≻ B ≻ F ≻ A ∼ G ≻ D ≻ E
where H is most preferred, E is least preferred, and A and G are equally linked. Prove that your utility function gets the correct utility ranking of bundles. (Hint: Try utility functions of Cobb-Douglas form)
(b) (2 points) Come up with a new bundle, called bundle I, that has the same utility level as bundle E but has different quantities of good x and good y AND has more of good x than it does of good y. Explain clearly how your bundle I satisfies these requirements.
(c) (12 points) Graph and label bundles A − I on the following grid. Graph the indifference curves that go through each point and specify the utility level of each indifference curve. Make sure to label the bundle, the utility level, the axis, and to number the axis.
(d) (3 points) Give an example of another utility function that represents the same preferences that you came up with in part (a). Explain how two functions can represent the same preferences.
2. (30 points) Husky has the following preferences over coffee (x) and tea (y)
u(x,y) = min(3x,2y)
(a) (6 points) Are Husky’s preferences, rational (complete and transitive) and con- tinuous? Explain/prove your answer and state the definitions for completeness, transitivity, and continuity.
(b) (5 points) Are Husky’s preferences monotone? If yes, are they strongly monotone or weakly monotone? Define weak and strong monotonicity and then prove your answer.
(c) (3 points) Are Husky’s preferences strictly convex? Prove your answer.
(d) (10 points) Graph Husky’s indifference curves that go through points (2 , 3), (4, 6), (6, 9), (8, 12). Be sure to label the axis and the utility levels of the indifference curves. (Hint: You should be graphing 4 indifference curves.)
(e) (4 points) On the same graph above, draw a budget constraint where px = 2, py = 2, and m = 20. Note that careful attention to precise graphing here will help in part (f).
Draw on the graph above
(f) (2 points) Subject to the budget constraint you drew above, graphically solve for the utility maximization bundle (x* , y* ) for this consumer. (Although we haven’t discussed the utility maximization special cases, Leontief and Linear, in lecture 3 yet, you should still be able to identify the optimal bundle graphically.)
3. (20 points) Graph the budget constraints described in each of these situations Be sure to show your calculations!
(a) (5 points) Suppose you are at a small chocolate shop. There are milk chocolate truffles (x) and dark chocolate truffles (y). You have $20 to spend and both truffles are $2 each. Graph the budget constraint on the graph below.
(b) (5 points) A stressed out student trying to decide where to take yoga classes. They have $36 to spend on yoga classes this month. At SuperStrength yoga studio (x), the first 4 yoga classes are free. After that, SuperStrength yoga classes are $12 each. At the university gym (y), yoga classes come out to be about $3 per yoga class. Graph the budget constraint on the graph below.
(c) (5 points) Let the price of a new magic lotion (x) be $4 per ounce for the first 83/1 = 3/25 ounces, and then $0.16 per ounce after that. The corresponding face wash (y) has a flat price of $1 per ounce. The consumer has $40 to spend on their new skincare regimen. Graph their budget constraint below.
(d) (5 points) If the people in parts (a)-(c) all had rational, strictly convex and strongly monotone utility functions, such as u(x,y) = √xy , do you expect there always to be a unique utility maximizing bundle for parts (a)-(c), respectively? Explain. (No calculation needed)
4. (15 points) Suppose there is a consumer that is trying to solve the following optimiza-tion problem:
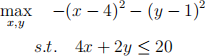
(a) (9 points) Use the Lagrangian method to solve the above utility maximization problem. That is, jump straight to setting up the Lagrangian and solving.
(b) (6 points) Are the demands you solved for in part a the utility maximizing values for x and y? If yes, explain. If no, what are the utility maximizing values for x and y and why did the Lagrangian not give you the correct answer?
5. (20 points) Solve the utility maximization problem for a consumer with the following preferences over the many steps (for full credit you must show your work.)
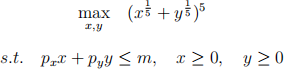
Note that px , pg , mare just placeholders for numbers, meaning, you should treat them as constants. The variables of the problem are x and y.
(a) (3 points) We always want to setup the problem first. Since the setup is already given in the question, identify the objective function and the constraint(s).
(b) (6 points) Then we need to check if we can use the Lagrangian method and if the solution to the Lagrangian will be optimal before setting up and solving the Lagrangian. In other words, is the budget constraint binding and are the sufficient conditions for interior solutions satisfied?
(c) (11 points) After verifying the conditions in part (b), use the Lagrangian method to solve the above utility maximization problem. What is the demand for good x* (px ,py , m) and good y* (px ,py , m)?