CISC235
Winter 2024
Assignment 1
Deadline: Jan 26, 2024, 11:59 PM
In this assignment you will implement a Stack class and then use it to write non-recursive versions of recursive algorithms.
Part 1:
Implement a Stack class based on using a one-dimensional array to hold the stack elements. When created, every Stack should use a 10-element array.
The Stack class must allow the push, pop, and isEmpty operations. However the push operation must check to see if the array is full before adding the new value. If the array is full, push must create a new array that is bigger than the current one, copy the existing stack into the new array, and then add the new value at the end.
There are different strategies for choosing the size of the new array. One popular method is to double the size of the existing array. Thus if the original 10-element array is filled, it is replaced by a 20-element array. If that fills, the new replacement array has 40 elements, etc.
An alternative strategy is to increase the size of the array by a constant amount each time it needs to grow.
There is a trade-off: if you grow by potentially large increments (as in the doubling strategy) you run the risk of allocating far more space than is needed. But if you grow by small increments, you may have to repeat the grow op (haha) very frequently.
Why not just make the array huge at the start? Memory is cheap, isn’t it? Yes, but it’s never a good idea to be wasteful with resources. The more compact our solutions are, the easier it will be to implement them in environments where resources are scarce. We don’t want to have a huge array sitting around mostly empty.
For your implementation, choose any growth strategy that seems reasonable. The study of optimizing this process is fascinating but outside of the scope of CISC-235. You may want to look up the strategy that Python uses for its built-in list data structure (which is really just an array in disguise).
Part 2:
Consider this recursive function that takes an integer
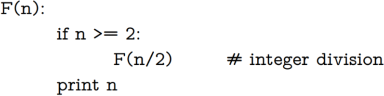
Using a stack, we can write a non-recursive function to get the same result:

Perform the same transformation on each of the following recursive functions (there are four). For each one, write a non-recursive equivalent function that uses your Stack class.
Run the given algorithms and your non-recursive versions on the specified data for each function to demonstrate that they are equivalent. Either write the output to a file or save it with a screenshot. The file or screenshot must have your name and student number visible.
Include this evidence of correctness in your submitted zip file.
Function 1:
This recursive function prints the famous Collad sequence, starting at any given positive integer n. (Actually it prints the sequence in reverse order.)
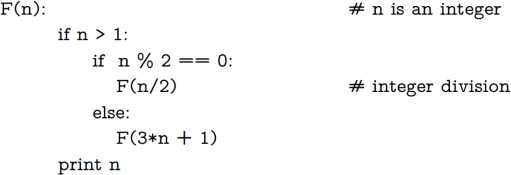
Show the results of running the original F(n) and your non-recursive function on all values in the set {7,18,19,22,105}
Function 2:
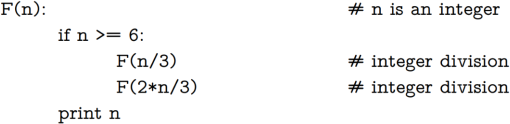
Show the results of running the original F(n) and your non-recursive function on all values in the set {7,18,19,22,43}
Note: for Functions 3 and 4, you may want to redefine your Stack so that each element of the stack consists of a pair of integers.
Function 3:
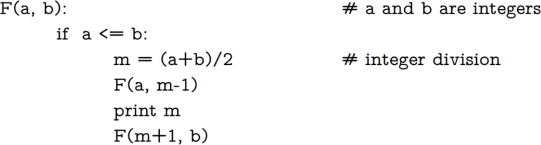
Show the results of running the original F(n) and your non-recursive function on these pairs of values {0,7),1,18),4,19),(-1,22)}
Function 4:
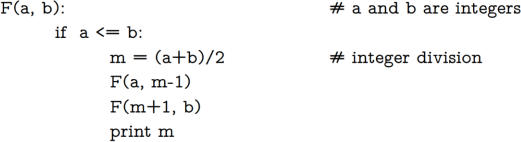
Show the results of running the original F(n) and your non-recursive function on these pairs of values {0,7),,18),,19),(-1,22)}
Part 3:
In Part 1 you chose a strategy for increasing the size of the array used to hold the Stack elements. Using the four functions that you wrote in Part 2 as evidence, would you now say that your choice was a good one? Why or why not? You may want to apply complexity analysis to explain your decision.
Logistics:
You may complete the programming part of this assignment in Python.
You must submit your source code, properly documented according to standards established in CISC-121 and CISC-124. You must also submit the evidence that your non-recursive functions are correct. Your source code must contain the following statement: “I
confirm that this submission is my own work and is consistent with the Queen's regulations on Academic Integrity.”
Combine your files into an Assigment1.zip file for uploading.
You are required to work individually on this assignment. You may discuss the problem in general terms with others and brainstorm ideas, but you may not share code. This includes letting others read your code or your written conclusions. You are allowed to use ChatGPT, but you should share links containing your conversation with ChatGPT for reference.
Submission will be through onQ Assignment 1 dropbox.