QTM 347 HW2

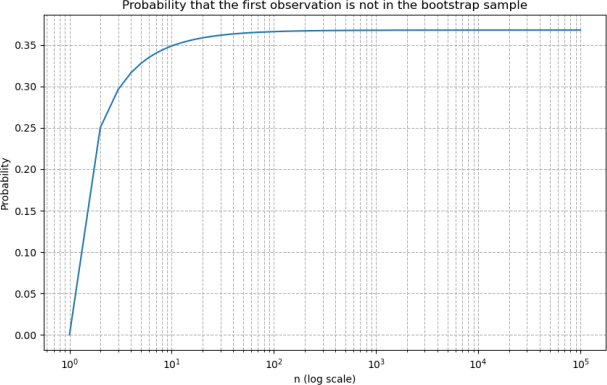
We can see a pattern of convergence.  This pattern illustrates an important concept in bootstrap sampling:  as the size of the original sample increases, the probability of any specific observation being omitted from a bootstrap sample approaches a limit.  This reflects the balance between the increasing number of opportunities for an observation to be included in the bootstrap sample and the constant probability of it being selected in any single draw.

0.2 Problem 2:

[ ]: college = load_data("College")

college["Accept.Rate"] = college["Accept"]/college["Apps"]

college = college .drop("Accept", axis=1)

college = college .drop("Apps", axis=1)

[ ]: ## a)

mu_hat = college["Accept.Rate"] .mean()

mu_hat

[ ]: 0.7469277072775414

[ ]: ## b)

standard_error= college["Accept.Rate"] .std()/np .sqrt(len(college["Accept .

↪Rate"]))

print("The estimated standard error is: ",standard_error)

The estimated standard error is:  0.005277323728707518

[ ]: ## c)

def boot_mean(X, B=1000, seed=0):

rng = np .random .default_rng(seed)

first_, second_ = 0, 0

n = X .shape[0]

print("mean", np .mean(X))

for _ in range(B):

idx = rng .choice(n, n, replace=True)

value = np .mean(X .loc[idx])

first_ += value

second_ += value**2

return np .sqrt(second_ / B - (first_ / B)**2)

se_mu_hat_bootstrap=boot_mean(college["Accept.Rate"])

mean 0.7469277072775414

[ ]: ## d)

from scipy.stats import ttest_1samp

from scipy import stats

import statsmodels.api as sm

[ ]: confidence_interval = [mu_hat - 2*se_mu_hat_bootstrap, mu_hat +␣ ↪2*se_mu_hat_bootstrap]

confidence_interval

[ ]: [0.7364686641045017, 0.7573867504505811]

[ ]: t_statistic, p_value = ttest_1samp(college[ 'Accept.Rate '], mu_hat)

se = np .std(college["Accept.Rate"]) / np .sqrt(len(college["Accept.Rate"]))

df = len(college["Accept.Rate"]) - 1

t_critical = stats .t .ppf(0.975, df)

confidence_interval_ttest = (mu_hat - t_critical * se, mu_hat + t_critical * se)

print("confidence interval from ttest is␣

↪ ",confidence_interval_ttest,"\nconfidence indeterval from bootstrap␣ ↪ is",confidence_interval)

confidence interval from ttest is  (0.7365748535300279, 0.7572805610250549)

confidence indeterval from bootstrap is [0.7364686641045017, 0.7573867504505811]

The  confidence  intervals  from  the  one-sample  t-test  and  the  bootstrap  method  are  very  close, indicating consistent estimates for the mean acceptance rate.   This similarity suggests that the bootstrap method is a robust alternative to the traditional t-test approach.  Differences between the intervals can be attributed to the variability in bootstrap resampling and the approximation methods  used.   The  bootstrap  method  is  less  reliant  on  distributional  assumptions,  making  it versatile for various data types. Both methods provide reliable evidence about the mean acceptance rate, demonstrating the effectiveness of these statistical tools in analysis.

[ ]: ## e)

def boot_OLS(X, Y, B=1000, seed=0):

rng = np .random .default_rng(seed)

n = X .shape[0]

first_, second_ = np .zeros((2,)), np .zeros((2,))

for _ in range(B):

idx = rng .choice(n, n, replace=True)

Y_ = Y .loc[idx]

X_ = X .loc[idx]

# add constant

X_ = sm .add_constant(X_)

# sm.OLS does not automatically include an intercept term

value = sm .OLS(Y_, X_) .fit() .params .values

first_ += value

second_ += value * value

return np .sqrt(second_ / B - (first_ / B)**2)

se_beta = boot_OLS(college["Top10perc"], college["Accept.Rate"])

print(f"Bootstrap standard errors: Intercept ( 0): {se_beta[0]}, Coefficient␣ ↪ ( 1): {se_beta[1]}")

Bootstrap standard errors: Intercept ( 0): 0.00934089871787182, Coefficient

( 1): 0.0003245674075839749

[ ]: ## f)

X = sm .add_constant(college["Top10perc"])

Y = college["Accept.Rate"]

model = sm .OLS(Y, X) .fit()

se_beta 0 ols = model .bse[0]

se_beta 1 ols = model .bse[1]

print(f"Standard error of intercept ( 0): {se_beta 0 ols}")

print(f"Standard error of coefficient ( 1): {se_beta 1 ols}")

Standard error of intercept ( 0): 0.00860399673826018

Standard error of coefficient ( 1): 0.00026300038151207936

The bootstrap standard errors are slightly higher than those calculated using the standard formula in sm.OLS().  This discrepancy can occur due to the bootstrap method’s nature, which involves resampling with replacement to create many  “pseudo-datasets.”   These pseudo-datasets capture the variability in the data, potentially leading to slightly higher estimated standard errors if the original dataset has certain peculiarities or is not perfectly representative of the population.

[ ]: ## g)

from sklearn.neighbors import KNeighborsRegressor

[ ]: def bootstrap_knn_se(X, y, predict_point, n_bootstrap=1000, k_neighbors=10,␣ ↪ seed=0):

rng = np .random .default_rng(seed)

predictions = []

# Ensure X and y are numpy arrays

X = X .values

y = y .values

for _ in range(n_bootstrap):

# Bootstrap sampling

indices = rng .choice(len(X), len(X), replace=True)

X_sample, y_sample = X[indices], y[indices]

# Reshape X_sample for scikit-learn compatibility

X_sample_reshaped = X_sample .reshape(-1, 1)

# KNN regression

knn = KNeighborsRegressor(n_neighbors=k_neighbors)

knn .fit(X_sample_reshaped, y_sample)

# Predicting for Top10perc=76

pred = knn .predict(np.array([[predict_point]]))

predictions .append(pred[0])

# Compute standard error (standard deviation of bootstrap predictions)

return np .std(predictions, ddof=1)

se_pred_accept_rate = bootstrap_knn_se(college["Top10perc"], college["Accept .

↪Rate"], 76, n_bootstrap=1000, k_neighbors=10, seed=42)

se_pred_accept_rate

[ ]: 0.03400926935401351

[ ]: se_pred_accept_rate_5 = bootstrap_knn_se(college["Top10perc"], college["Accept .

↪Rate"], 76, n_bootstrap=1000, k_neighbors=5, seed=42)

se_pred_accept_rate_50 = bootstrap_knn_se(college["Top10perc"], college["Accept .

↪Rate"], 76, n_bootstrap=1000, k_neighbors=50, seed=42)

print("K= 5 provide a SE of ",se_pred_accept_rate_5,"\nK=50 provide a SE␣ ↪of",se_pred_accept_rate_50)

K= 5 provide a SE of  0.038934844284861866

K=50 provide a SE of 0.02894815513257801

Lower  K  (K=5)  results  in  a  higher  standard  error.   This  suggests  that  with  fewer  groups  (or resamples), there’s more variability in the estimate.  This could be because each group has to cover a wider range of the data, leading to less precise estimates.

Intermediate K  (K=10) shows a reduction in standard error compared to K=5,  indicating that increasing the number of groups (or resamples) can lead to more stable and reliable estimates, as the variability due to random sampling is reduced.

Higher K (K=50) further reduces the standard error to the lowest level among the three scenarios. This indicates that as K increases, the precision of the estimate improves, likely due to the increased granularity in sampling or cross-validation. Each subset of the data is smaller, leading to potentially more  accurate  and  less  variable  estimates  of the  model’s  performance  or  the  parameter  being estimated.

0.3 Problem 3

[ ]: college[ 'Private_numeric '] = college[ 'Private '] .map({ 'Yes ' : 1, 'No ' : 0})

[ ]: import pandas as pd

import statsmodels.api as sm

# Assuming 'college' is your DataFrame and it's already loaded

response = college[ 'Accept.Rate ']

predictors = college .columns .drop([ 'Accept.Rate ', 'Private ']) # Exclude the␣

↪ response and original Private column

best_r2_a = -float("inf")

best_model_a = None

# (a) Best Subset Selection for One-Predictor Model

for predictor in predictors:

X = sm .add_constant(college[[predictor]]) # Ensure X is a DataFrame

model = sm .OLS(response, X) .fit()

if model .rsquared > best_r2_a:

best_r2_a = model .rsquared

best_model_a = (predictor, model)

print(f"Best one-predictor model is based on {best_model_a[0]} with R^2 =␣ ↪{best_r2_a}")

Best one-predictor model is based on Top10perc with R^2 = 0.22913012842545943

0.3.1 (b)

[ ]: from itertools import combinations

best_r2_b = -float("inf")

best_model_b = None

best_predictors_b = None

# Generate all combinations of two predictors

for predictor_pair in combinations(predictors, 2):

X = sm .add_constant(college[list(predictor_pair)]) # Make sure to convert␣ ↪ the tuple to a list

model = sm .OLS(response, X) .fit()

if model .rsquared > best_r2_b:

best_r2_b = model .rsquared

best_model_b = model

best_predictors_b = predictor_pair

print(f"Best two-predictor model is based on {best_predictors_b} with R^2 =␣ ↪{best_r2_b}")

Best two-predictor model is based on ('Top10perc', 'Private_numeric') with R^2 = 0.2566214603917484

0.3.2 (c)

[ ]: best_predictor_a = best_model_a[0] # Assuming this is the best predictor from␣ ↪part (a)

best_r2_c = best_r2_a # Start with the R^2 from the best one-predictor model best_model_c = best_model_a[1] # And the model itself

best_predictors_c = best_predictor_a # Start with the best single predictor

# Iterate over the remaining predictors to find the best two-predictor model

for predictor in predictors:

if predictor != best_predictor_a: # Skip the predictor used in the best␣

↪ one-predictor model

X = sm .add_constant(college[[best_predictor_a, predictor]])

model = sm .OLS(response, X) .fit()

if model .rsquared > best_r2_c:

best_r2_c = model .rsquared

best_model_c = model

best_predictors_c = (best_predictor_a, predictor)

print(f"Best two-predictor model (forward stepwise) is based on␣ ↪{best_predictors_c} with R^2 = {best_r2_c}")

Best two-predictor model (forward stepwise) is based on ('Top10perc',

'Private_numeric') with R^2 = 0.2566214603917484

0.3.3 d

In part (a), I fit 15 models. In part (b), I fit 105 models considering all pairs of predictors. In part (c), using forward stepwise selection, at least 29 models are fitted in the process to find the best two-predictor model.

The fact that the best two-predictor model is the same regardless of the selection method (exhaus-  tive search vs. forward stepwise) indicates that  “Top10perc” and  “Private__numeric” are strong  predictors when used together compared to other combinations or individual predictors.  The in-  crease  in  R2R^2R2  from  the  best  one-predictor  to  the  two-predictor  model  shows  that  adding  “Private__numeric” provides a significant incremental predictive value beyond what “Top10perc” offers alone.

0.4 Problem 4

0.4.1 a)

[ ]: from sklearn.model_selection import train_test_split, KFold

[ ]: X = college .drop([ 'Accept.Rate ', 'Private '], axis=1)

y = college[ 'Accept.Rate ']

# Splitting the dataset into training (80%) and test (20%) sets

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,␣ ↪random_state=50)

0.4.2 b)

[ ]: from sklearn.linear_model import LinearRegression

from sklearn.metrics import mean_squared_error

# Fitting the linear regression model

linear_model = LinearRegression()

linear_model .fit(X_train, y_train)

# Making predictions on the test set

y_pred_linear = linear_model .predict(X_test)

# Calculating and reporting the test MSE

linear_test_mse = mean_squared_error(y_test, y_pred_linear)

print(f"Linear Regression Test MSE: {linear_test_mse}")

Linear Regression Test MSE: 0.019270389442537825

0.4.3 c)

[ ]: from sklearn.linear_model import ElasticNetCV

from sklearn.preprocessing import StandardScaler

from sklearn.pipeline import Pipeline

from sklearn.metrics import mean_squared_error

import matplotlib.pyplot as plt

[ ]: import sklearn.linear_model as skl

lambdas = 10**np .linspace(8, -2, 100) / y_train .std()

college[ 'Accept.Rate ']

kfold = KFold(n_splits=5, shuffle=True, random_state=50)

ridgeCV = ElasticNetCV(alphas=lambdas, l1_ratio=0, cv=kfold)

scaler = StandardScaler()

pipeCV = Pipeline(steps= [( 'scaler ', scaler), ( 'ridge ', ridgeCV)])

pipeCV .fit(X_train, y_train)

y_pred = pipeCV .predict(X_test)

test_mse = mean_squared_error(y_test, y_pred)

print(f"Test MSE: {test_mse}")

tuned_ridge = pipeCV .named_steps[ 'ridge ']

best_alpha = tuned_ridge .alpha_

print(f"Best alpha ( ) selected by cross-validation: {best_alpha}")

Test MSE: 0.019265604345980403

Best alpha ( ) selected by cross-validation: 0.08932201930628549

0.4.4 d)

[ ]: lambdas = 10**np .linspace(8, -2, 100) / y_train .std()

K = 5

kfold = KFold(K, random_state=50, shuffle=True)

lassoCV = ElasticNetCV(n_alphas=100, l1_ratio=1, cv=kfold)

scaler = StandardScaler(with_mean=True, with_std=True)

pipeCV = Pipeline(steps= [( 'scaler ', scaler), ( 'lasso ', lassoCV)])

pipeCV .fit(X_train, y_train)

tuned_lasso = pipeCV .named_steps[ 'lasso ']

optimal_alpha_lasso = tuned_lasso .alpha_

non_zero_coefs = np .sum(tuned_lasso .coef_ != 0)

y_pred_lasso = pipeCV .predict(X_test)

mse_test_lasso = mean_squared_error(y_test, y_pred_lasso)

print(f"Optimal alpha ( ) for Lasso: {optimal_alpha_lasso}")

print(f"Test MSE for Lasso Regression: {mse_test_lasso}")

print(f"Number of non-zero coefficients: {non_zero_coefs}")

Optimal alpha ( ) for Lasso: 0.0015483071895745686