CS 189/289A Introduction to Machine Learning
Spring 2024 Jonathan Shewchuk
HW2: I love Math
Due Wednesday, February 7 at 11:59 pm
• Homework 2 is an entirely written assignment; no coding involved.
• We prefer that you typeset your answers using LATEX or other word processing software. If you haven’t yet learned LATEX, one of the crown jewels of computer science, now is a good time! Neatly handwritten and scanned solutions will also be accepted.
• In all of the questions, show your work, not just the final answer.
• Start early. This is a long assignment. Most of the material is prerequisite material not covered in lecture; you are responsible for finding resources to understand it.
Deliverables:
1. Submit a PDF of your homework to the Gradescope assignment entitled “HW2 Write-Up”. You may typeset your homework in LATEX or Word (submit PDF format, not .doc/.docx format) or submit neatly handwritten and scanned solutions. Please start each question on a new page. If there are graphs, include those graphs in the correct sections. Do not put them in an appendix. We need each solution to be self-contained on pages of its own.
• In your write-up, please state whom you had discussions with (not counting course staff)
about the homework contents.
• In your write-up, please copy the following statement and sign your signature next to it. (Mac Preview, PDF Expert, and FoxIt PDF Reader, among others, have tools to let you sign a PDF file.) We want to make it extra clear so that no one inadvertently cheats. “I certify that all solutions are entirely in my own words and that I have not looked at another student’s solutions. I have given credit to all external sources I consulted.”
1 Identities and Inequalities with Expectation
For this exercise, the following identity might be useful: for a probability event A, P(A) = E[1{A}], where 1{·} is the indicator function.
1. For any non-negative real-valued random variable X and constant t > 0, show that P(X ≥ t) ≤ E[X]/t.
This is known as Markov’s inequality.
Hint: show that for a, b > 0, 1{a ≥ b} ≤ a/b.
2. A common use for concentration inequalities (like Markov’s inequality above) is to study the performance of a statistical estimator. For example, given a random real-valued variable Z with true mean µ and variance 1, we hope to estimate its mean using the regular estimator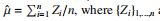
are n Independent and identically distributed (i.i.d.) real values sampled from the distribution. Using Markov’s inequality above, please show that
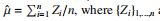are n Independent and identically distributed (i.i.d.) real values sampled from the distribution. Using Markov’s inequality above, please show that
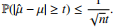
This tells us that the more samples we have, the better our estimator will be.
Hint: Use reverse Jensen’s inequality to convert the mean of an absolute value into a mean of squares.
2 Probability Potpourri
1. Recall that the covariance of two random variables X and Y is defined to be Cov(X, Y) = E[(X − E[X])(Y − E[Y])]. For a multivariate random variable Z (i.e., each component of
the vectorZ is a random variable), we define the square covariance matrix Σ with entriesΣi j = Cov(Zi
, Zj). Concisely, Σ = E[(Z − µ)(Z − µ)
⊤
], where µ is the mean value of the(column) vector Z. Show that the covariance matrix is always positive semidefinite (PSD).
You can use the definition of PSD matrices in Q3.2.
2. The probability that an archer hits her target when it is windy is 0.4; when it is not windy, herprobability of hitting the target is 0.7. On any shot, the probability of a gust of wind is 0.3.
Find the probability that
(i) on a given shot there is a gust of wind and she hits her target.
(ii) she hits the target with her first shot.
(iii) she hits the target exactly once in two shots.
(iv) on an occasion when she missed, there was no gust of wind.
3. An archery target is made of 3 concentric circles of radii 1/
√
3, 1 and √
3 feet. Arrows striking within the inner circle are awarded 4 points, arrows within the middle ring are awarded 3 points, and arrows within the outer ring are awarded 2 points. Shots outside the target areawarded 0 points.
Consider a random variable X, the distance of the strike from the center in feet, and let theprobability density function of X be
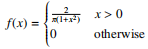
What is the expected value of the score of a single strike?
3 Linear Algebra Review
1. First we review some basic concepts of rank. Recall that elementary matrix operations do not change a matrix’s rank. Let A ∈ R
m×n
and B ∈ R
n×p
. Let In denote the n × n identity matrix.
(a) Perform elementary row and column operations1
to transform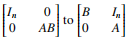
.
.
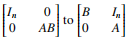(b) Let’s find lower and upper bounds on rank(AB). Use part (a) to prove that rank A + rank B − n ≤ rank(AB). Then use what you know about the relationship between the column space (range) and/or row space of AB and the column/row spaces for A and B to argue that rank(AB) ≤ min{rank A, rank B}.
(c) If a matrix A has rank r, then some r × r submatrix M of A has a nonzero determinant.
Use this fact to show the standard facts that the dimension of A’s column space is at least r, and the dimension of A’s row space is at least r. (Note: You will not receive credit for other ways of showing those same things.)
(d) It is a fact that rank(A
⊤A) = rank A; here’s one way to see that. We’ve already seen in part (b) that rank(A
⊤A) ≤ rank A. Suppose that rank(A
⊤A) were strictly less than rank A.
What would that tell us about the relationship between the column space of A and the null space of A
⊤
? What standard fact about the fundamental subspaces of A says that relationship is impossible?
(e) Given a set of vectors S ⊆ R
n
, let AS = {Av : v ∈ s} denote the subset of R
m
found by applying A to every vector in S . In terms of the ideas of the column space (range) and row space of A: What is AR
n
, and why? (Hint: what are the definitions of column space and row space?) What is A
⊤AR
n
, and why? (Your answer to the latter should be purely in terms of the fundamental subspaces of A itself, not in terms of the fundamental subspaces of A
⊤A.)
2. Let A ∈ R
n×n be a symmetric matrix. Prove equivalence between these three different defi nitions of positive semidefiniteness (PSD). Note that when we talk about PSD matrices, they are defined to be symmetric matrices. There are nonsymmetric matrices that exhibit PSD properties, like the first definition below, but not all three.
(a) For all x ∈ R
n
, x
⊤Ax ≥ 0.
(b) All the eigenvalues of A are nonnegative.
(c) There exists a matrix U ∈ R
n×n
such that A = UU⊤
.
Positive semidefiniteness will be denoted as A ⪰ 0.
3. The Frobenius inner product between two matrices of the same dimensions A, B ∈ R
m×n
is
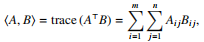
where trace M denotes the trace of M, which you should look up if you don’t already know it. (The norm is sometimes written ⟨A, B⟩F to be clear.) The Frobenius norm of a matrix is
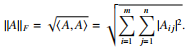
Prove the following. The Cauchy–Schwarz inequality, the cyclic property of the trace, and the definitions in part 2 above may be helpful to you.
(a) x
⊤Ay = ⟨A, xy⊤
⟩ for all x ∈ R
m
, y ∈ R
n
, A ∈ R
m×n
.
(b) If A and B are symmetric PSD matrices, then trace (AB) ≥ 0.
(c) If A, B ∈ R
n
×
n
are real symmetric matrices with
λmax(A) ≥ 0 and B being PSD, then
⟨
A, B⟩ ≤
√
n
λ
max
(A)∥B∥F.
Hint:
Construct a PSD matrix using
λmax(A)
4. Let A ∈
R
m
×
n
be an arbitrary matrix. The maximum singular value of
A is defined to be
σmax(A
) =
√
λ
max
(A⊤A) =
√
λmax(AA⊤). Prove that
σmax(A) =
max
u ∈R
m
,
v
∈
R
n
∥u∥
=
1,
∥
v
∥=
1
(u
⊤Av).
HW2: I r Math, ©UCB CS 189/289A, Spring 2024. All Rights Reserved. This may not be publicly shared without explicit permission. 54 Matrix/Vector Calculus and Norms
1. Consider a 2 × 2 matrix A, written in full as
A
11
A
12
A
21
A
22
, and two arbitrary 2-dimensional
vectors x, y. Calculate the gradient of
sin(A
2
11 + e
A11+A22 ) + x
⊤Ay
with respect to the matrix A.
Hint: The gradient has the same dimensions as A. Use the chain rule.
2. Aside from norms on vectors, we can also impose norms on matrices. Besides the Frobenius
norm, the most common kind of norm on matrices is called the induced norm. Induced norms
are defined as
∥A∥p = sup
x, 0
∥
Ax
∥
p
∥
x∥
p
where the notation ∥ · ∥p on the right-hand side denotes the vector ℓp-norm. Please give the
closed-form (or the most simple) expressions for the following induced norms of A ∈ R
m×n
.
(a) ∥A∥2. (Hint: Similar to Question 3.4.)
(b) ∥A∥∞.
3. (a) Let α =
n
P
i
=
1
y
i
ln
β
i for
y, β
∈
R
n
. What are the partial derivatives
∂α
∂β
i
?
(b) Let γ = A
ρ
+
b
for
b ∈
R
n
, ρ
∈
R
m
, A ∈ R
n×m
. What are the the partial derivatives
∂γi
∂ρ
j
?
(c) Given x ∈ R
n
, y ∈ R
m
,
z ∈ R
k
and y = f(x), f : R
n
7→ R
m
, z = g(y), g : R
m
7→ R
k
. Please
write the Jacobian
dz
dx
as the product of two other matrices. What are these matrices?
(d) Given x ∈ R
n
, y,z ∈ R
m
, and y = f(x),z = g(x). Write the gradient ∇xy
⊤
z in terms of y
and z and some other terms.
4. Let’s apply the multivariate chain rule to a “simple” type of neural network called a linear
neural network. They’re not very powerful, as they can learn only linear regression functions
or decision functions, but they’re a good stepping stone for understanding more complicated
neural networks. We are given an n × d design matrix X
. Each row of X is a training point,
so X represents n training points with
d features each. We are also given an
n × k matrix Y.
Each row of Y is a set of k labels for the corresponding training point in X. Our goal is to
learn a k × d matrix W of weights2
such that
Y ≈ XW⊤
.
2The reason for the transpose on W⊤
is because we think in terms of applying W to an individual training point. Indeed, if
X
i
∈ R
d
and Yi ∈ R
k
respectively denote the i-th rows of X and Y transposed to be column vectors, then we can write Yi ≈ WXi
. For
historical reasons, most papers in the literature use design matrices whose rows are sample points, rather than columns.
HW2: I r Math, ©UCB CS 189/289A, Spring 2024. All Rights Reserved. This may not be publicly shared without explicit permission. 6If n is larger than d, typically there is no W that achieves equality, so we seek an approximate
answer. We do that by finding the matrix W that minimizes the cost function
RSS(W) = ∥XW⊤ − Y∥
2
F
.
(1)
This is a classic least-squares linear regression problem; most of you have seen those before.
But we are solving k linear regression problems simultaneously, which is why Y and W are
matrices instead of vectors.
Linear neural networks.
Instead of optimizing W over the space of k
× d matrices directly,
we write the W we seek as a product of multiple matrices. This parameterization is called a
linear neural network.
W = µ(WL, WL−1, . . . , W2, W1) = WLWL−1 · · · W2W1.
Here, µ is called the matrix multiplication map (hence the Greek letter mu) and each Wj
is a
real-valued dj × d
j−1 matrix. Recall that W is a k × d matrix, so dL = k and d0 = d. L is the
number of layers
of “connections” in the neural network. You can also think of the network
as having L + 1 layers of units: d0 = d units in the input layer, d1 units in the first hidden
layer, dL−1 units in the last hidden layer, and dL = k units in the output layer.
We collect all the neural network’s weights in a weight vector θ = (WL, WL−1, . . . , W1) ∈ R
dθ
,
where dθ = dLdL−1 + dL−1dL−2 + . . . + d1d0 is the total number of real-valued weights in the
network. Thus we can write µ(θ) to mean µ(WL, WL−1, . . . , W1). But you should imagine θ as
a column vector: we take all the components of all the matrices WL, WL−1, . . . , W1 and just
write them all in one very long column vector. Given a fixed weight vector θ, the linear neural
network takes an input vector x ∈ R
d0 and returns an output vector y = WLWL−1 · · · W2W1 x =
µ(θ)x ∈ R
dL
.
Now our goal is to find a weight vector θ that minimizes the composition RSS ◦ µ—that is, it
minimizes the cost function
J(θ) = RSS(µ(θ)).
We are substituting a linear neural network for W and optimizing the weights in θ instead
of directly optimizing the components of W. This makes the optimization problem harder
to solve, and you would never solve least-squares linear regression problems this way in
practice; but again, it is a good exercise to work toward understanding the behavior of “real”
neural networks in which µ is not a linear function.
We would like to use a gradient descent algorithm to find θ, so we will derive ∇θJ as follows.
(a) The gradient G = ∇WRSS(W) is a k × d matrix whose entries are Gi j = ∂RSS(W
)/∂W
i j
,
where RSS(W) is defined by Equation (1). Write two explicit formulas for ∇W
RSS(
W
).
First, derive a formula for each Gi j using summations, simplified as much as possi
ble. Use that result to find a simple formula for ∇WRSS(W) in matrix notation with no
summations.
HW2: I r Math, ©UCB CS 189/289A, Spring 2024. All Rights Reserved. This may not be publicly shared without explicit permission. 7(b) Directional derivatives are closely related to gradients. The notation RSS′
∆W(W) de
notes the directional derivative of RSS(W) in the direction ∆W, and the notation µ
′
∆θ
(θ)
denotes the directional derivative of µ(θ) in the direction ∆θ.
3
Informally speaking, the
directional derivative RSS′
∆W(W) tells us how much RSS(W) changes if we increase W
by an infinitesimal displacement ∆W ∈ R
k×
d
. (However, any ∆W we can actually spec
ify is not actually infinitesimal; RSS′
∆W
(W
) is a local linearization of the relationship
between W and RSS(W) at W. To a physicist, RSS′
∆W(W) tells us the initial velocity of
change of RSS(W) if we start changing W with velocity ∆W.)
Show how to write RSS′
∆W(W) as a Frobenius inner product of two matrices, one related
to part (a).
(c) In principle, we could take the gradient ∇θ µ(θ), but we would need a 3D array to express
it! As I don’t know a nice way to write it, we’ll jump directly to writing the directional
derivative µ
′
∆θ
(θ). Here, ∆θ ∈ R
dθ
is a weight vector whose matrices we will write
∆θ = (∆WL, ∆WL−1, . . . , ∆W1). Show that
µ
′
∆θ
(θ) =
L
X
j=1
W>j∆WjW<j
where W>j = WLWL−1 · · · Wj+1, W<j = W
j−
1
Wj−2 · · ·
W1
, and we use the convention that
W>L is the dL × dL identity matrix and
W
<
1
is the
d0 ×
d
0 identity matrix.
Hint: although µ is not a linear function of θ, µ is linear in any single Wj
; and any
directional derivative of the form µ
′
∆θ
(θ) is linear in ∆θ (for a fixed θ).
(d) Recall the chain rule for scalar functions, d
d
x
f(g(x))|x=x0 = d
d
y
f(y)|y=g(x0)
·
d
d
x
g(x)|x=x0
.
There is a multivariate version of the chain rule, which we hope you remember from
some class you’ve taken, and the multivariate chain rule can be used to chain directional
derivatives. Write out the chain rule that expresses the directional derivative J
′
∆
θ
(θ)|θ=θ0
by composing your directional derivatives for RSS and µ, evaluated at a weight vec
tor θ0. (Just write the pure form of the chain rule without substituting the values of those
directional derivatives; we’ll substitute the values in the next part.)
(e) Now substitute the values you derived in parts (b) and (c) into your expression for J
′
∆
θ
(θ)
and use it to show that
∇θJ(θ) = (2 (µ(θ) X
⊤ − Y
⊤
)XW<
⊤
L
, . . . ,
2W>
⊤
j
(µ(θ) X
⊤ − Y
⊤
)XW<
⊤
j
, . . . ,
2W>
⊤
1
(µ(θ) X
⊤ − Y
⊤
)X).
This gradient is a vector in R
dθ written in the same format as (WL, . . . , Wj
, . . . , W1). Note
that the values W>j and W<j here depend on θ.
Hint: you might find the cyclic property of the trace handy.
3
“∆W” and “∆θ” are just variable names that remind us to think of these as small displacements of W or θ; the Greek letter delta
is not an operator nor a separate variable.
HW2: I r Math, ©UCB CS 189/289A, Spring 2024. All Rights Reserved. This may not be publicly shared without explicit permission. 85. (Optional bonus question worth 1 point. This question contains knowledge that goes be
yond the scope of this course, and is intended as an exercise to really make you comfort
able with matrix calculus). Consider a differentiable function f : R
n
7→ R. Suppose this
function admits a unique global optimum x
∗ ∈ R
n
. Suppose that for some spherical region
X
=
{x | ∥x − x
∗
∥
2 ≤ D} around x
∗
for some constant
D, the Hessian matrix H of the function
f(x
) is PSD and its maximum eigenvalue is 1. Prove that
f(x) − f(x
∗
) ≤
D
2
for every x ∈ X. Hint: Look up Taylor’s Theorem with Remainder. Use Mean Value Theorem
on the second order term instead of the first order term, which is what is usually done.
HW2: I r Math, ©UCB CS 189/289A, Spring 2024. All Rights Reserved. This may not be publicly shared without explicit permission. 95 Properties of the Normal Distribution (Gaussians)
1. Prove that E[e
λX
] = e
σ
2λ
2
/2
, where λ ∈
R is a constant, and X ∼ N(0
, σ2
). As a function of λ,
MX(λ) = E[e
λX
] is also known as the
moment-generating function
.
2. Concentration inequalities are inequalities that place upper bounds on the likelihood that
a random variable X is far away from its mean µ, written P(|X − µ| ≥ t), with a falling
exponential function ae−bt2
having constants a, b > 0. Such inequalities imply that
X is very
likely to be close to its mean µ. To make a tight bound, we want a to be as small and b to be
as large as possible.
For t > 0 and X ∼ N(0, σ2
), prove that P(X ≥ t) ≤ exp(−t
2
/2σ
2
), then show that P(|X| ≥ t) ≤
2 exp(−t
2
/2σ
2
).
Hint: Consider using Markov’s inequality and the result from Question 5.1.
3. Let X1, . . . , Xn ∼ N(0, σ2
) be i.i.d. (independent and identically distributed). Find a concen
tration inequality, similar to Question 5.2, for the average of
n Gaussians: P(
1
n
P
n
i=1 Xi ≥ t)?
What happens as n → ∞?
Hint: Without proof, use the fact that linear combinations of i.i.d. Gaussian-distributed vari
ables are also Gaussian-distributed. Be warned that summing two Gaussian variables does
not mean that you can sum their probability density functions (no no no!).
4. Let vectors u, v ∈ R
n
be constant (i.e., not random) and orthogonal (i.e.,
⟨u,
v⟩
=
u
· v
=
0).
Let X = (X1, . . . ,
X
n) be a vector of
n i.i.d. standard Gaussians, Xi ∼ N
(0
, 1)
,
∀
i
∈
[
n].
Let ux =
⟨u, X⟩ and vx = ⟨v, X⟩. Are ux and vx
independent? Explain. If
X
1, . . . ,
X
n
are
independently but not identically distributed, say
X
i ∼ N(0, i), does the answer change?
Hint: Two Gaussian random variables are independent if and only if they are uncorrelated.
HW2: I r Math, ©UCB CS 189/289A, Spring 2024. All Rights Reserved. This may not be publicly shared without explicit permission. 106 The Multivariate Normal Distribution
The multivariate normal distribution with mean µ ∈ R
d
and positive definite covariance matrix
Σ ∈ R
d×d
, denoted N(µ, Σ), has the probability density function
f(x; µ, Σ) =
1
p
(2π)
d
|Σ|
exp
−
1
2
(x − µ)
⊤Σ
−1
(x − µ)
! .
Here |Σ| denotes the determinant of Σ. You may use the following facts without proof.
• The volume under the normal PDF is 1.
Z
Rd
f(x) dx =
Z
Rd
1
p
(2π
)
d
|Σ|
exp ( −
1
2
(x − µ)
⊤Σ
−1
(x − µ)
) dx = 1.
• The change-of-variables formula for integrals: let f be a smooth function from R
d → R, let
A
∈ R
d×d be an invertible matrix, and let
b ∈ R
d be a vector. Then, performing the change of
variables
x 7→ z = Ax + b,
Z
Rd
f(x) dx =
Z
Rd
f(A
−1
z − A
−1
b) |A
−1
| dz.
1. Let X ∼ N(µ, Σ). Use a suitable change of variables to show that E[X] = µ.
2. Use a suitable change of variables to show that Var(X) = Σ, where the variance of a vector
valued random variable X is
Var(X) = Cov(X, X) = E[(X − µ) (X − µ)
⊤
] = E[XX⊤
] − µ µ⊤
.
Hints: Every symmetric, positive semidefinite matrix Σ has a symmetric, positive definite
square root Σ
1/2
such that Σ = Σ1/2Σ
1/2
. Note that Σ and Σ
1/2
are invertible. After the change
of variables, you will have to find another variance Var(Z); if you’ve chosen the right change
of variables, you can solve that by solving the integral for each diagonal component of Var(Z)
and a second integral for each off-diagonal component. The diagonal components will re
quire integration by parts.
HW2: I r Math, ©UCB CS 189/289A, Spring 2024. All Rights Reserved. This may not be publicly shared without explicit permission. 117 Gradient Descent
Consider the optimization problem min
x∈Rn
1
2
x
⊤Ax − b
⊤
x, where A ∈ R
n×n
is a PSD matrix with
0 < λmin(A) ≤ λmax(A) < 1.
1. Find the optimizer x
∗
(in closed form).
2. Solving a linear system directly using Gaussian elimination takes O(n
3
) time, which may be
wasteful if the matrix A is sparse. For this reason, we will use gradient descent to compute
an approximation to the optimal point x
∗
. Write down the update rule for gradient descent
with a step size of 1 (i.e., taking a step whose length is the length of the gradient).
3. Show that the iterates x
(k)
satisfy the recursion x
(k) − x
∗ = (I − A)(x
(k−1) − x
∗
).
4. Using Question 3.4, prove ∥
Ax∥2 ≤ λmax(A)∥x∥2.
Hint: Use the fact that, if λ
is an eigenvalue of
A, then λ
2
is an eigenvalue of A
2
.
5. Using the previous two parts, show that for some 0 < ρ < 1,
∥x
(k) − x
∗
∥2 ≤ ρ∥x
(k−1) − x
∗
∥2.
6. Let x
(0) ∈
R
n be the starting value for our gradient descent iterations. If we want a solution
x
(k)
that is
ϵ >
0 close to x
∗
, i.e. ∥x
(k) − x
∗
∥2 ≤ ϵ, then how many iterations of gradient descent
should we perform? In other words, how large should
k be? Give your answer in terms of
ρ,∥x
(0) − x
∗
∥2, and ϵ.
HW2: I r Math, ©UCB CS 189/289A, Spring 2024. All Rights Reserved. This may not be publicly shared without explicit permission. 12