CS 188
Introduction to Artificial Intelligence
Spring 2023
Final
Q1. [12 pts] Search and Slime
Slowmo the snail is trying to find a path to a goal in an N × M grid maze. The available actions are to move one square up, down, left, right, and each action costs 1. Moves into walls are impossible. The goal testis a black-box function (the snail does not knowhow the function works) that returns true if its state argument is a goal state, and false otherwise.
(a) [1 pt] Assume that there is a reachable goal state. Which algorithms are complete for this problem? Select all that apply.
■ Breadth-first tree search ■ Uniform-cost tree search ■ A∗ graph search with h = 0
■Depth-first tree search ■ A∗ tree search with h = 0 ■ None of the above
(b) [1 pt] Assume that there is a reachable goal state. Which algorithms are optimal for this problem? Select all that apply.
■ Breadth-first tree search ■ Uniform-cost tree search ■ A∗ graph search with h = 0
■Depth-first tree search ■ A∗ tree search with h = 0 ■ None of the above
(c) [2 pts] Assume that there may or may not be a reachable goal state. Which algorithms are complete for this problem? Select all that apply.
■Breadth-first tree search ■Uniform-cost tree search ■ A∗ graph search with h = 0
■Depth-first tree search ■A∗ tree search with h = 0 ■ None of the above
For the rest of the question, consider a modified version of the search problem:Slowmo the snail hates entering squares that are already covered in his own slime trail. This means that an action is impossible if it would enter a square that Slowmo has previously entered. There may or may not be a reachable goal state in this problem.
(d) [2 pts] What is the size of the state space (in terms of N and M) required to correctly reflect this modified problem?
(e) [2 pts] In this modified problem, which algorithms are complete? Select all that apply.
■ Breadth-first tree search ■ Uniform-cost tree search ■ A∗ graph search with h = 0
■ Depth-first tree search ■ A∗ tree search with h = 0 ■ None of the above
(f) [2 pts] In this modified problem, which algorithms are optimal? Select all that apply.
■ Breadth-first tree search ■ Uniform-cost tree search ■ A* graph search with ℎ = 0
■ Depth-first tree search ■ A* tree search with ℎ = 0 ■ None of the above
(g) [2 pts] Consider an arbitrary search problem. We want to modify this search problem so that the agent is not allowed to move into a state more than once.
Which of the following changes to the original problem, each considered in isolation, correctly represents this modifica- tion? Select all that apply.
■ Change the successor function to disallow actions that move into a previously-visited state.
■ Add a list of visited states in the state space, and also change the successor function to disallow actions that move into a previously-visited state.
■ Change the goal test to return false if a state has been visited more than once.
■ Add a list of visited states in the state space, and also change the goal test to return false if a state has been visited more than once.
■ None of the above
Q2. [11 pts] Searching for a Path with a CSP
We have a graph with directed edges between nodes. We want to find a simple path (i.e. no node is visited twice) between node s and node g.
We decide to use a CSP to solve this problem. The CSP has one variable for each edge in the graph: the variable Xvw represents whether the edge between node v and node w is part of the path. Each variable has domain {true, false}.
In each of the next three parts, a constraint is described; select the logical expression that represents the constraint. Notation:
• N(v) is the set of all neighbors of node v. (Recall: anode w is a neighbor of v iff there is an edge from v to w).
• The function ExactlyOne() returns an expression that is true iff exactly one of its inputs is true.
•vxi∈S xi refers to the conjunction of all xi in the set S.
•⋁xi∈S xi refers to the disjunction of all xi in the set S.
(a) [2 pts] The starting nodes has a single outgoing edge in the path and no incoming edge in the path.
- ExactlyOne({Xsv ∣ v ∈ N(s)})∧vv∈N(s) ¬Xvs o ExactlyOne({Xsv ∣ v ∈ N(s)}) ∧vv∈N(s) Xvs
- ExactlyOne({Xvs ∣ v ∈ N(s)})∧vv∈N(s) ¬Xsv o ExactlyOne({Xvs ∣ v ∈ N(s)}) ∧vv∈N(s) Xsv
(b) [2 pts] The goal node g has a single incoming edge in the path and no outgoing edge in the path.
|
o ExactlyOne({Xgv ∣ v ∈ N(s)})∧ vv∈N(g) ¬Xvg |
o ExactlyOne({Xgv ∣ v ∈ N(s)}) ∧vv∈N(g) Xvg |
|
|
o ExactlyOne({Xvg ∣ v ∈ N(s)}) ∧vv∈N(g) Xgv |
(c) [2 pts] If node v has an incoming edge in the path, then it must have exactly one outgoing edge in the path.
- vw∈N(v) Xwv ⟺ ExactlyOne({Xvw ∣ w ∈ N(v)})
- vw∈N(v) Xwv ⟹ ExactlyOne({Xvw ∣ w ∈ N(v)})
- ⋁w∈N(v) Xwv ⟺ ExactlyOne({Xvw ∣ w ∈ N(v)})
- ⋁w∈N(v) Xwv ⟹ ExactlyOne({Xvw ∣ w ∈ N(v)})
Suppose we set up our CSP on a graph with nodes s, a, b,c, d, e,g. We want to run a hill climbing algorithm to maximize the number of satisfied constraints. Sideways steps (variable changes that don’t change the number of satisfied constraints) are allowed. All variables in the CSP initially set to false.
(e) [2 pts] Assuming that each of the following variables exists in the CSP, select all variables that might be set to true in the first step of running hill-climbing.
■ Xsa ■ Xsb □ Xcs □ Xab □ Xde ■ Xeg 。 None of the above
(f) [1 pt] Will our hill-climbing algorithm always find a solution to the CSP if one exists?
- Yes, the algorithm will incrementally add edges to the path until the path connects s and g.
- Yes, the algorithm will eventually search overall combinations of assignments to the variables until a satisfying one is found.
- No, the search will sometimes find a solution to the CSP that is not a valid path.
- No, the search will sometimes fail to satisfy all of the constraints in the CSP.
Q3. [9 pts] A Multiplayer MDP
Alice and Bob are playing a game on a 2-by-2 grid, shown below. To start the game, a puck is placed on square A.
At each time step, the available actions are:
• Up, Left, Down, Right: These actions move the puck deterministically. Actions that move the puck off the grid are disallowed. These actions give both players a reward of 0.
• Exit: This action ends the game. Note that the Exit action can be taken no matter where the puck is. This action gives Alice and Bob rewards depending on the puck’s final location, as shown below.
Each player tries to maximize their own reward, and does not care about what rewards the other player gets.
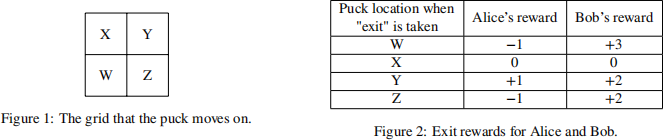
(a) [2 pts] Suppose Bob is the only player taking actions in this game. Bob models this game as an MDP with a discount factor 0 < Y ≤ 1.
For which of the following states does Bob’s optimal policy depend on the value of Y? Select all that apply.
□ W ■ Y 。 None of the above.
□ X ■ Z
For the rest of the question, Alice and Bob alternate taking actions. Alice goes first.
Alice models this game with the following game tree, and wants to run depth-limited search with limit 3 turns. She uses an evaluation of 0 for any leaf node that is not a terminal state. (Note: Circles do not necessarily represent chance nodes.)
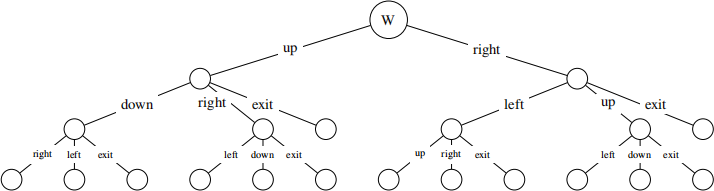
(b) [1 pt] This is a zero-sum game.
。 True . False
(c) [1 pt] What is Alice’s value of the root node of the tree?
(d) [1 pt] What is Bob’s value of the root node of the tree?
(e) [2 pts] Assuming that Alice and Bob play optimally, what are possible sequences of actions that they might play? Select all that apply.
|
■ |
up,right, exit |
□ |
right, up, exit |
|
□ |
up,right, down |
□ |
right, exit |
|
□ |
right, left, right |
。 |
None of the above. |
Alice instead decides to model the game as an MDP. Assumptions:
• = 0.5
• Alice knows Bob’s policy is .
• D(s, a) represents the new state you move into when you start at states and take action a.
(f) [2 pts] Fill in the blanks to derive a modified Bellman equation that Alice can use to compute the values of states. Lets′ = D(s, a) and s′′ = D(s′ , (s′ )).
V(s) = m![]() x R(s, a, s′ ) + (i) (ii) + (iii) (iv)
x R(s, a, s′ ) + (i) (ii) + (iii) (iv)
(i) 。 1 . 0.5 。 0.25
(ii) 。 0 。 R(s, (s), s′ ) . R(s′ , (s′ ), s′′ )
(iii) 。 1 。 0.5 . 0.25
(iv) 。 V(s) 。 V(s′ ) . V(s′′ )
Q4. [13 pts] Slightly Different MDPs
Each subpart of this question is independent.
For all MDPs in this question, you may assume that:
• The maximum reward for any single action is some fixed number R > 0, and the minimum reward is 0.
• The discount factor satisfies 0 < ≤ 1.
• There are a finite number of possible states and actions.
(a) [2 pts] Which statements are always true? Select all that apply.
□ ∑s∈S T(s, a, s′ ) = 1.
■ ∑s′ ∈S T(s, a, s′ ) = 1.
□ ∑a∈A T(s, a, s′ ) ≤ 1.
□ For allstate-action pairs (s, a), there exists some s′ , such that T(s, a, s′ ) = 1.
。 None of the above
(b) [2 pts] Which statements are always true? Select all that apply.
■ Every MDP has aunique set of optimal values for each state.
□ Every MDP has a unique optimal policy.
□ If we change the discount factor of an MDP, the original optimal policy will remain optimal.
■ If we scale the reward function r(s, a) of an MDP by a constant multiplier > 0, the original optimal policy will remain optimal.
。 None of the above
(c) [2 pts] Which statements are true? Select all that apply.
■ Policy iteration is guaranteed to converge to a policy whose values are the same as the values computed by value iteration in the limit.
■ Policy iteration usually converges to exact values faster than value iteration.
□ Temporal difference (TD) learning is off-policy.
■ An agent is performing Q-learning, using a table representation of Q (with all Q-values initialized to 0). If this agent takes only optimal actions during learning, this agent will eventually learn the optimal policy.
。 None of the above
(d) [2 pts] We modify the reward function of an MDP by adding or subtracting at most from each single-step reward.
(Assume > 0.)
We fix apolicy , and compute V (s), the values of all states s in the original MDP under policy . Then, we compute V′ (s), the values of all states in the modified MDP under the same policy .
What is the maximum possible difference | V′ (s) − V (s)| for any states?
。
。
. Σ![]() = ∕(1 − )
= ∕(1 − )
。 R
。 None of the above
(e) [3 pts] We modify the reward function of an MDP by adding exactly C to each single-step reward. (Assume C > 0.) Let V and V′ be the optimal value functions for the original and modified MDPs. Select all true statements.
■ For all states s, V′ (s) − V(s) = ∑![]() = C∕(1 − ).
= C∕(1 − ).
□ For all states s, V′ (s) − V(s) = C.
□ For some MDPs, the difference V′ (s) − V(s) may vary depending on s.
。 None of the above
(f) [2 pts] We notice that an MDP’s state transition probability T(s, a, s′ ) does not depend on the action a.
Can we derive an optimal policy for this MDP without computing exact or approximate values (or Q-values) for each state?
![]() Yes, because the optimal policy for this MDP can be derived directly from the reward function.
Yes, because the optimal policy for this MDP can be derived directly from the reward function.
。 Yes, because policy iteration gives an optimal policy and does not require computing values (or Q-values). 。 No, because we need a set of optimal values (or Q-values) to do policy extraction.
。 No, because there is no optimal policy for such an MDP.
。 None of the above
Q5. [8 pts] Bayes’ Nets
The head of Pac-school is selecting the speaker (S) for the commencement ceremony, which depends on the student’s major (M), academic performance (A), and confidence (C). The student’shard work (H) affects their academic performance (A), and academic performance (A) can affect confidence (C).
(a) [1 pt] Select all of the well-formed Bayes’ nets that can represent a scenario consistent with the assertions given above
(even if the Bayes’ net is not the most efficient representation).
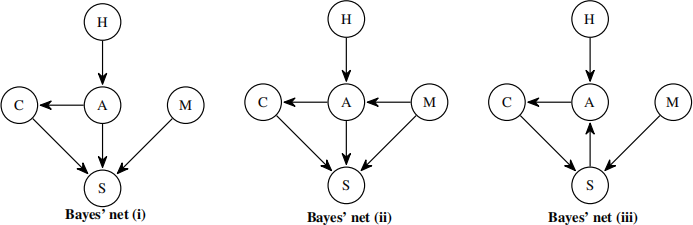
■ Bayes’ net (i) □ Bayes’ net (iii)
■ Bayes’ net (ii) 。 None of the above
For the rest of the question, consider this Bayes net with added nodes Fearlessness (F) and Voice (V).
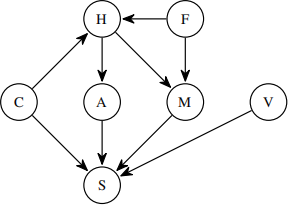
(b) [2 pts] Select all the conditional independence expressions that follow from the two standard axioms (1) a variable is independent of its non-descendants given its parents, and (2) a variable is independent of everything else given its Markov blanket.
■ F ⟂⟂ C □ H ⟂⟂ S | C, A, M 。 None of the above
■ M ⟂⟂ C | H, F ■ F ⟂⟂ A | H, M
The Bayes’ net,repeated for your convenience:
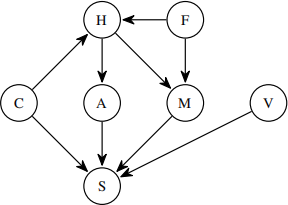
Assume all the variables have a domain size of 2. Consider the query P(S| +h, +v, +f) in the Bayes net from the previous part.
(c) [1 pt] Suppose the query is answered by variable elimination, using the variable ordering C, A,M. What is the size (number of entries) of the largest factor generated during variable elimination? (Ignore the sizes of the initial factors.)
。 21 . 23 。 25
。 22 。 24 。 26
(d) [2 pts] If we use Gibbs sampling to answer this query, what other variables need to be referenced when sampling M?
■ H ■ F 。 None of the above
■ A ■ M
■ S ■ C
Now suppose the CPT for variable A is as follows, and assume there are no zeroes in any other CPT.
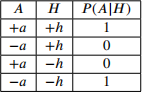
Hint: Recall that one requirement for Gibbs sampling to converge is that, in the limit of infinitely many samples, every state with non-zero probability is sampled infinitely often, regardless of the initial state.
(e) [1 pt] Will Gibbs sampling converge to the correct answer for the query P(S | + f)?
。 Yes, because convergence properties of Gibbs sampling depend only on the structure of Bayes net, not on the values in the CPTs.
。 Yes, but it will converge very slowly because of the 0s and 1s in the CPT.
. No, because some states with non-zero probability are unreachable from other such states.
。 No, because Gibbs sampling always fails with deterministic CPTs like this one.
。 None of the above
(r) [1 pt] Will Gibbs sampling converge to the correct answer for the query P(s | + h, +![]() , +f)?
, +f)?
。 Yes, because convergence properties of Gibbs sampling depend only on the structure of Bayes net, not on the values in the CPTs.
。 Yes, but it will converge very slowly because of the 0s and 1s in the CPT.
。 No, because some states with non-zero probability are unreachable from other such states.
。 No, because Gibbs sampling always fails with deterministic CPTs like this one.
![]() None of the above
None of the above