Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
MATH 152
Exam 1
1) An object is moving with a velocity function v(t) = sin2 (πt) − 4/3, where tis measured in minutes. Setup (but do not solve) an integral expression that would express the total distance traveled by the object on the interval [0, 2/1].
2) Determine whether the statements are true or false, and explain why:
a. An integration constant (+C) is necessary to evaluate a definite integral.
b. The area under the curve f(x) = x/1 from x = 1 to infinity is finite.
c. 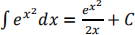
d. An integral of the form ∫ sinn x cosm x dx, where n and mare both even, must be solved using power-reduction identities.
3) Create your own example of a rational function of the following form:
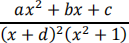
Where the four constants a, b, c, dare all distinct non-zero integers, two negative and two positive. Then, find the antiderivative of your function by first finding the partial fractions.
Integrals Section – Choose three problems to do from this section. Simplify the integrals if possible before evaluating: factor, perform basic algebra steps, make any appropriate substitutions, etc.. At each step, be sure to explain what you are doing, and why. If you do more than three, you can getup to 5 points extra credit for each additional problem!
