COM00038H
BEng, BSc, MEng and MMath Degree Examinations 2022–23
Computer Science
Computer Vision & Graphics
1 (16 marks) Perspective projection
(i) [3 marks] The intrinsic matrix of a camera C is given by

What do the symbols f , cx and cy represent in terms of camera C?
(ii) [13 marks] The intrinsic parameters of camera C are f = 300, cx = 320, cy = 240. The extrinsic pose parameters of camera C are given by the matrix R and the vector t.
(a) [2 marks] Let xi be animage point in homogeneous coordinates. What is the meaning of the term homogeneous in this context?
(b) [3 marks] What do the symbols R and t represent?
(c) [8 marks] Let xi(′) = K−1xi where both xi and xi(′) are in homogeneous image
coordinates. The x-component of xi(′) is represented by xi(′) and they-component by yi(′). In
the special case when R is the identity matrix, the vector t should satisfy the equation At = y where
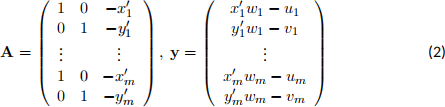
Table 1 gives three image points and their corresponding locations in world coordinates.

Table 1: Table of image points and their corresponding world points
Estimate the vector t.
2 (15 marks) Digital cameras and colour spaces
A 12-patch colour target, uniformly lit by a D65 illuminant, is measured using a tele-colorimeter. The tele-colorimeter measurements, represented as xyY values, are reported in table 2, where each column refers to adifferent patch. The firstrow reports the x colour coordinate, the second row corresponds toy and the third row to Y :

A photograph of the same colour target has been taken with a digital camera (12-bit ADC). The de-bayered digital values are given in table 3, where the first row refers to the red channel, the second row to the green channel and the last row to the blue channel. As in table 2, each column refers to a specific patch out of the 12 in the colour target.

(i) [10 marks] Compute the matrix M required to map camera data to linear sRGB, using the tele-colorimeter data as ground truth. Describe all the steps required to get to the matrix from the given input data.
(ii) [5 marks] Apply the colour correction matrix to the camera data. Encode the colours as
16-bit linear sRGB values. Which colour corrected value shows the largest distance with respect to the corresponding reference value, if computing the distance within the linear sRGB cube?
3 (14 marks) Binocular Stereo
(i) [4 marks] Two images are taken of the same scene with a stereo camera. The fundamental matrix relating the two images is given by

A point in the left image is given by x and the corresponding point in the right image is given by x′ . By considering x′T Fx, or otherwise, show that the image pair is rectified.
(ii) [10 marks] The cameras are fronto-parallel with a translation between optical centres of 100mm in the x-direction and 0 in they- and z-directions. The optical centre and focal length of both cameras are (500,500) pixels and 35mm respectively, and the sensor has 100 pixels per mm.
(a) [6 marks] If a point (x,y) in the left image corresponds to a point (x′ , y) in the right image, then show that

where w is the depth of the point in camera coordinates. Give the value of α .
(b) [4 marks] Point (150,675) in the left image and (325,675) in the right image are found to be matching in the stereo image pair. Find the 3D position of the scene point, in the coordinate system of the left camera.
4 (18 marks) Reflectance models
In this question you will compute the value of some analytical Bidirectional Reflectance
Distribution Function (BRDF) models for a given set of parameters. All vectors are expressed in the local reference frame.
(i) [10 marks] Compute the value of the Oren-Nayar BRDF for the following sets of
parameters. For each point, also write down the components of the halfway vector to three significant figures:
• Viewing vector: vr : (θr = π/4,ϕr = 3π/2); Lighting direction: vi : (θr = π/4,ϕr = π/2); diffuse albedo = 0.6; σ = π/6;
• Viewing vector: vr = [−0.936, −0.341, 0.087]; Lighting direction:
vi = [−0.168, −0.951, 0.259]; diffuse albedo = 0.9; σ = 2π/9;
(ii) [8 marks] Consider a flat teflon sample (refractive index η = 1.35). Given the viewing
vector vr : (θr = 13π/36,ϕr = 3π/2), compare the value of the Fresnel reflectance using the Schlick’s approximation (parameterised in terms of difference angle) with the value given by the Cook-Torrance approximation, for the following viewing directions:
• vi : (θi = 9/2π, ϕi = 3/2π);
• vi = [−0.492, 0.853, 0.174].
5 (17 marks) Volumetric representations and Machine Learning
(i) [4 marks] Explain the concept of a signed distance function (SDF) and describe how it can be used in neural networks to learn about shapes.
(ii) [4 marks] An SDF representing a 3D object is given by
s(u,v, w) = 2uv + 2uw − 14 (5)
The point (2, 3, a) lies on the surface of the object. Calculate the value of a and the unit surface normal of the object at this point.
(iii) [4 marks] You are given the task of training a deep neural network to learn the SDF for a shape. The network is represented by f(x;Θ) where x is a 3D position and Θ contains the network parameters. You are given a set of pairs (xi, d) containing a 3D point and the signed distance to the closest point on the surface. Propose a cost function for training the network.
(iv) [5 marks] You are given a set of images of the object instead of point clouds. Explain, in general terms, how you might use the concept of self-supervision to learn the SDF, and what extra elements you would need to add.
6 (20 marks) Ray tracing
In this question, you will trace the path of a ray within a scene. The only objects contained in the scene area transparent slab and a sphere, both with smooth surfaces. The coordinates of the vertices of the slab are given in table 4; the sphere has radius sr = 5, and the coordinates of its center c are: c(10, 5, −3). Figure 1 shows the coordinate system and a view of the scene on the x − y plane.

(i) [12 marks] Consider the ray with origin po(−14, −4, 0) and direction d = [0.853, 0.523, 0]. Assume the slab is made of a transparent material with Index Of Refraction (IOR) equal to 1.81. Compute the coordinates of the intersection points between the ray and the sphere.
(ii) [8 marks] Consider the ray with origin po(−12, −4.6, 0) and direction d = [0.820, 0.572, 0]. Assume the slab is made of a transparent material with Index Of Refraction (IOR) equal to 1.31. Compute the coordinates of the intersection points between the ray and the sphere.
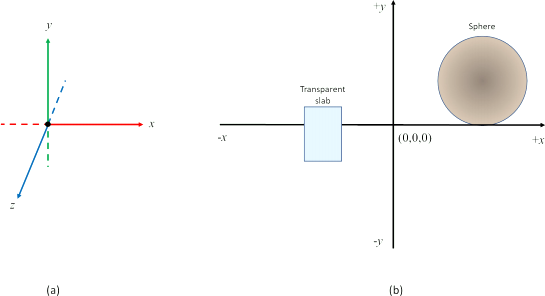
Figure 1: Coordinate system (a) and orthographic view of the scene in the x-y plane (b).