COMP4161 2023 T3
Advanced Topics in Software Verification
Assignment 3
This assignment starts on Thursday, 2023-11-09 and is due on Monday, 2023-11-20, 23:59h. We will accept Isabelle .thy files only. You are allowed to make late submissions up to five days (120 hours) after the deadline, but at a cost: -5 marks per day. For a proof to receive marks, it must be processed by Isabelle without errors. Use the sorry command for partial proofs. In addition to this pdf document, please refer to the provided Isabelle template for the definitions and lemma statements.
This assignment should be completed using Isabelle2023 and AutoCorres 1.10.
https://github.com/seL4/l4v/releases/download/autocorres-1.10/autocorres-1.10.tar.gz
You will need a Unix-based machine, AutoCorres does not support native Windows. Linux, Mac, and Windows WSL should work.
After extracting the autocorres-1.10.tar.gz archive, load the template theory files via e.g. L4V_ARCH=ARM isabelle jedit -d
The assignment is take-home. This does NOT mean you can work in groups. Each submission is personal. For more information, see the plagiarism policy: https://student.unsw.edu.au/plagiarism
Submit using give on a CSE machine: give cs4161 a3 a3.thy
For all questions, you may prove your own helper lemmas, and you may use lemmas proved earlier in other questions. You can also use automated tools like sledghammer. If you can’t finish an earlier proof, use sorry to assume that the result holds so that you can use it if you wish in a later proof. You won’t be penalised in the later proof for using an earlier true result you were unable to prove, and you’ll be awarded partial marks for the earlier question in accordance with the progress you made on it.
1 Huffman Code (62 marks)
A Huffman code is an algorithm for lossless compression. Given a distribution of the relative frequency of each character, the algorithm assigns the most frequent character the shortest encoding. The encoding, a stream of bits, is a so-called variable-length prefix code. A code is a prefix code when no two symbols are encoded as a prefix of the other.
As an example for Huffman encoding, consider the sequence of symbols abcdaa.The frequency of the occurrence of the symbol a is 3, while that of each other symbol is 1. In this case, Huffman code will encode a with the shortest code (e.g. True), and all other symbols with longer codes, starting with False.
In this assignment we will define Huffman encoding and decoding in Isabelle, and prove, that under the right conditions, decoding an encoded sequence of symbols will yield back the original sequence of symbols.
As the first step of computing a Huffman code, we define a function freq_list that computes the frequency of each symbol in a given sequence. We leave the alphabet of symbols open as a type variable 'a. The input sequence to this function is not necessarily exactly the text that we will later encode, it is merely a text corpus that has the expected alphabet and distribution of letters in this alphabet.
Throughout this question, the template lists helper lemmas that you can prove and use, but do not have to. They are marked with the oops command instead of sorry.
(a) Define the function freq_of that produces a list of pairs, in which the first component is the symbol and the second component the number of times the symbol occurs in the input list. Test the function with a few examples. For concrete test cases, you can use the type string in Isabelle, which is defined as char list. Concrete strings are written with two single quotes, e.g. ''abc''. (4 marks)
(b) Prove that each character is mentioned only once in the result of freq_of. (6 marks)
Given a frequency list of symbols, we can then construct the so-called Huffman tree. The paths in the Huffman tree will give us the code for each symbol while ensuring the prefix-property and keeping track of the frequency of symbols.
datatype 'a htree = Leaf 'a int | Branch "'a htree" "'a htree"
The template gives the full definition of the Huffman tree construction. It first sorts the frequency list, converts it into a list of Leaf trees, and then keeps merging sub-trees in this list by weight (frequency) until the list only contains one element. This element is the resulting Huffman tree.
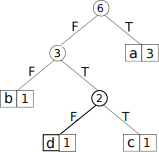
To turn the tree into a map of symbols to codes, we traverse the tree from the root, adding False to the output when we go left, and True when we go right. See function code_list in the template, which returns a list of pairs where the first component is the symbol, and the second component is the code (bool list) for that symbol. The function code_map flips the first and second components of such a list, so we can also translate codes back into symbols.
The Isabelle library function map_of turns such ('a 'b) lists into functions 'a ) 'b option,
also called map from 'a to 'b.
(c) Given a map 'a ) bool list option, write a function encoder that turns a list of symbols into code (a list of bool). You can assume that the map has a translation for all characters of the input. (4 marks)
(d) The template gives a definition for the corresponding decoder. It consumes one bit of input at a time, checking if the input consumed so far yields a valid code or not. If yes, it emits the corresponding symbol, if no, it keeps accumulating input.
Note that both encoder and decoder are so far independent of Huffman trees. They merely expect coding maps for single characters and translate them into functions for lists of characters. They will only behave correctly if the maps they get as input are inverse to each other, and if the code is indeed a prefix code. The domain dom of a map is the set of all inputs for which the output is not None.
Prove the following lemma (16 marks):
[[is_inv mp mp'; unique_prefix mp'; set xs 己 dom mp; [] ![]() dom mp']] =) decoder mp' [] (encoder mp xs) = xs
dom mp']] =) decoder mp' [] (encoder mp xs) = xs
(e) Show that the inverse of a map can be constructed by swapping the first and second com- ponents of the pairs in the list, if the lists are distinct in the first and second components: (6 marks)
[[distinct (map snd xs); distinct (map fst xs)]]
=) is_inv (map_of xs) (map_of (map (λ(a, b) . (b, a)) xs))
(f) Write a function letters_of that for any 'a htree returns the set of symbols 'a that is stored in its leaves. (4 marks)
(g) Write a function distinct_tree, analogous to distinct on lists, that decides whether the letters of an 'a htree are distinct from each other. (4 marks)
(h) Show that code_list turns any tree with with distinct letters into a list with distinct symbols in the first component. (6 marks)
(i) Show that if the characters of a frequency list are distinct, so are the letters of the corre- sponding Huffman tree. (12 marks)
2 Stack (38 marks)
In this question we will be verifying a simple stack implementation in C. The objective is to familiarise yourself with proofs about imperative programs and reasoning about finite machine word arithmetic in C.
The file stack.c contains a global array content of length LEN storing the contents of the stack (of type unsigned int). The global variable top is the index of the top-most element of the stack when the stack contains elements and -1 otherwise. Note that top is an unsigned int, which means that -1 is the same as MAX_INT.
To reason about the C functions, the assignment template defines an abstraction predicate is_stack xs s that is true if and only if the list xs contains the contents of the global stack in state s. The definition is based on the recursive definition stack_from xsn s that starts looking at the stack not from the top, but from index n instead.
After processing by AutoCorres, the template opens the context stack, in which monadic versions of the C functions are available under names ending with ', for instance pop' for the C function pop and so on. The global state is an Isabelle record with fields top_ '' and contents_ ''. The contents_ '' field is of Isabelle type array. Array types are written t[n] where t is the element type, and n is the size of the array. The type provides an Arrays.index function to access fields and an Arrays.update function to update elements. Array.index a i is written a.[i]. Use find_theorems to discover rules about the array type.
Finally, the C program operates on finite machine words, but some of our predicates operate on natural numbers. The function unat converts a machine word into a natural number. The operators < and on machine words can also be expressed via unat. Use find_theorems to discover rules about unat and its interactions with operators on natural numbers.
We begin the proof by showing same basic properties of the abstraction predicates:
(a) is_stack [] s = (top_ '' s = - 1) (2 marks)
(b) is_stack [] s = (is_empty' s = 1) (2 marks)
(c) stack_from xs (- 1) s = (xs = []) (2 marks)
(d) is_stack [x] s = (top_ '' s = 0 ∧ content_ '' s.[0] = x) (3 marks)
(e) is_stack (x # xs) s =(top_ '' s < LEN ∧content_ '' s.[unat (top_ '' s)] = x ∧ stack_from xs (top_ '' s - 1) s)(4 marks)
For C functions that change the state, we will want to know under which changes the predicate remains the same.
(f) The stack_from predicate takes the index as a parameter and therefore does not depend on the value of the variable top_ '':stack_from xs n (s(|top_ '' := t|)) = stack_from xs n s (5 marks)(g) The stack_from predicate also does not change if we update the array at an index that is outside of the range 0..n, for instance at n+1.
unat (n + 1) < LEN =⇒
stack_from xs n
(s(|top_ '' := n + 1, content_ '' := update (content_ '' s) (unat (n + 1)) x|)) = stack_from xs n s
The template contains an optional lemma that might help with induction over the xs. (6 marks)
We are now ready to prove properties of the C functions.
(h) Complete the Hoare logic statement in the assignment template and prove partial correct- ness of pop'. (4 marks)
(i) Complete the Hoare logic statement in the assignment template and prove total correctness of pop', using the {| }| ! syntax instead of {| }|. Total correctness means you will also have to show all side conditions that could lead to undefined behaviour in C. (4 marks)
(j) Complete the Hoare logic statement in the assignment template and prove total correctness of push'. (5 marks)
(k) Prove partial correctness of sum', which empties the stack and sums up all of its elements. The Isabelle function sum_list xs in the template stands for the sum of all elements of xs. It is easier in this proof to unfold the definition of pop' again than to use the previous correctness lemma. (7 marks)