Mathematical Software
CELEN085
Coursework Assignment: Spring Semester 2023/2024
Instructions: (Please read carefully)
1. This Coursework Assignment is worth 25% of your overall CELEN085 module marks.
2. The deadline for submission of the completed project assignment is 22 April, 2024.
3. Penalties for late submission will be applied in accordance with University regulations, ”I/We understand that 5 marks per working day will be deducted from the final mark for lateness, unless an extension form has been authorised and is attached, e.g. a mark of 42 minus 5 marks changes to 37” .
4. No excuses such as problems with internet connectivity, etc. will be entertained; so you are suggested to submit your working well in advance before the deadline.
5. This work must be completed on your own. Plagiarism and collusion are regarded as very serious academic offences and will be treated as such.
6. More marks will be gained for elegant and reasonably efficient solutions than for long and tedious ones.
7. Support in some form will be available from tutors, but you should not expect them to guide you through the entire solution. Please send your query by email to [email protected]
8. Please complete the Coursework Assignment Submission Form available on Moodle under the block“Coursework Assignment” and sign it (digital/handwritten signature in Chinese or English).
9. Zip all your files (Coursework Assignment Submission Form, Prob1.m, Prob2.m, Prob3.m, Prob1.png, Prob2.png, Prob3.png, CW.tex, and CW.pdf).
10. Name the zipped file as: N085 CW StudentID. zip![]()
![]() e.g. N085 CW 20XXXXXX.zip
e.g. N085 CW 20XXXXXX.zip![]()
![]()
11. Submit the zipped file electronically to the drop box available on module Moodle page. Please contact Module Convenor (Mr. Manish Dhyani) if you cannot find the drop box.
12. Note that your work will not be returned so you should keep a copy for reference.
Part I
Imagine a generous bank that pays 100% interest, you could turn $100 into $200 in one year. Now if this bank decides to pay the interest twice a year, you could turn $100 into $150 at the middle of the year, and $225 at the end of the investment year. Comparing with these two methods of investing, you get more money from the latter one, because you reinvest halfway through. And this is called compound interest. The formula for compound interest is shown below:
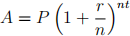
Where:
❼ t is the number of years.
❼ A is the final amount after t years.
❼ P is the principal amount (initial investment).
❼ r is the annual interest rate (decimal).
❼ n is the number of times the interest is compounded per year.
The compound interest is a very important theory in finance, and around the seventeenth century, Jocab Bernoulli, who was interested in the continuous compound interest, realized that with a fixed annual interest rate, when the compounding period became smaller and smaller, and the investment periods n became more and more, the amount of annual return eventually converged towards a limit.
To approximate this limit, in GeoGebra:
1. Create sliders for P , r, and t with suitable fixed values to represent the principal, annual interest rate and time in years respectively.
2. Create an integer slider n that starts from 0.
3. Define a function to calculate the final amount A as 
4. Define another function called countinuous compounding C as C = P · ert
5. Create a point B as (n, A), as the value of n increases, observe how point B approaches
the continuous compounding for various inputs.
Note: to achieve a better effect, adjust the ratio of x− and y− axis.
Save the file as Q1.ggb
From the above procedures, approximate the Euler’s Number e in the similar manner, and calculate the errors between your approximation and the exact e.
Note:
– Before starting, set the rounding as 15 Decimal Places for a better presentation.
– To directly show the error, create a TextBox on the graphing area to link the error.
Search “Text Tool” in GeoGebra Manual to see how to use this command.
Save the file as Q2.ggb
Part II
The previous way to approximate e is normally called Horizontal Asymptote. There is another way to approximate e with the help of factorials as shown below:
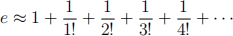
which comes from Taylor Expansion on the exponential functions.
To approximate e by factorial method:
1. Create a script file “Q3.m” in MATLAB.
2. Define a variable n as a vector with integer elements starting from 0 to 100.
3. Define a variable myE as the approximated e calculated based on n.
4. Plot the curves of the exact e and your approximated e in one figure and save the figure as “fig1.png” .
5. You should set appropriate figure caption and legends to achieve a better presentation.
6. Export the paired values of n and myE vertically into an Excel sheet named as “Approximation Data” .
Part III
Create a LATEX article document to summarise your work in approximating e (in Part I and Part
II). Your article must contain the following information:
1. Set the title as “Approximation of Euler’s Number”. Include your Student ID and display the title information. Once you have finished all sections in this article, display a table of contents after the title page.
2. Create a section “Introduction”. Include description about what is Euler Number.
3. Create a section “Analysis”. Brifely discuss the two approximation methods and underlying principles in mathematics in approximating e by these methods. In addition, you should include a table containing information in your approximation shown as below:
|
Number n |
Approx. e in Method I (10 d.p.) |
Approx. e in Method II (10 d.p.) |
|
5 |
|
|
|
10 |
|
|
|
50 |
|
|
|
100 |
|
|
4. Create a section “Conclusion”. Evaluate your approximation results and comment on the accuracy of e using both methods.
5. Create a section “Further discussion”. Summarise any further applications of using e.
Save your source code file as Q4.tex and generated PDF file as Q4.pdf.
Note that in your article, you are encouraged to include relevant mathematical contents and typeset them in good formats. it will help you improve your score.
Submission Checklist
Before online submission, make sure you have included the following documents in your zipped file.
1. Completed Project Submission Form
2. GGB files: Q1.ggb, Q2.ggb
3. MATLAB file: Q3. m
4. PNG file: fig1. png
5. TEX file: Q4. tex
6. PDF file: Q4. pdf