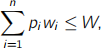Third Year Examination for the Degree of
Bachelor and Master of Engineering and Bachelor of Science
COMS-31900
Advanced Algorithms

Q1 .

(a) Explain the notion of an α-approximation for an optimisation problem. You should explain how the deinition changes between a maximisation and a minimisation prob-lem.[3 marks]
(b) Give the deinitions of the terms PTAS, FPTAS and APTAS. Clearly explain the diferences between the three.[6 marks]
(c) The Unbounded Knapsack problem is deined as follows.In the input there is a single knapsack (backpack) that has a weight limit W.There are also n distinct item types (numbered 1 to n).Each  item of type i has weight wi and value vi (both positive integers).There is an unlimited supply of each item type.The goal is to pack the highest total value of items into the knapsack without exceeding the weight limit. More formally, the goal is to maximize:

without exceeding the weight limit, i.e.

where pi is the number of packed items of type i (i.e. a non-negative integer) .

Note that the Unbounded Knapsack problem is not the same as the conventional (bounded) Knapsack problem. In the bounded version there is only one item of each type, whereas in the unbounded version you can pack as many items of each type as you like.

i. Find  the optimal  packing  in the  following example. You are  not  required to prove that it is optimal. There are three item types given by (w1  =  2, v1   = 3), (w2  = 3, v2  = 6) and (w3  = 4, v3  = 5) , and the weight limit is W = 35 . [1 mark]

ii. One possible approximation algorithm for the Unbounded Knapsack problem is as follows:  Let C be the current set of item types being considered.  Initially we consider all types, so C = f1, 2, . . . , ng.  Do the following:

.  Find the item type j in C with the highest value, i.e. aj such that

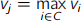
.  Pack as many items of type j as will it, without exceeding the weight limit W. This number could be zero.

.  Remove j from C and repeat (i.e.  do not attempt to pack items of type j again) if C is not empty.

.  The algorithm terminates when C is empty.

This algorithm can be implemented to run in O(n2 ) time.  However, its packing scheme is not very good!  Give a counter-example to show that this algorithm is not a 2-approximation. [5 marks]

iii.  Give a (correct) 2-approximation for the Unbounded  Knapsack problem de-scribed above.

Hint: You only need to pack items of one type. Which type should you pack?   [3 marks]

iv. Argue that the algorithm you gave in part iii) meets the deinition in part (a) .    [2 marks]

Q2 .   

(a)  Consider a set  H = fh1 , h2 , h3 g of hash functions.  Each function in  H maps a key from the set f1, 2, 3, 4g to a hash value in f1, 2, 3g. The explicit deinitions of the hash functions are given below:

h1 (1) = 1, h2 (1) = 2, h3 (1) = 1

h1 (2) = 3, h2 (2) = 1, h3 (2) = 3

h1 (3) = 2, h2 (3) = 3, h3 (3) = 2

h1 (4) = 3, h2 (4) = 2, h3 (4) = 3

i. What is the probability that h(1) = h(4), i.e.  Pr(h(1) = h(4)) , when h is picked uniformly at random from H? [3 marks]

ii.  Is  H a weakly universal set of hash functions? Justify your answer. [4 marks]

(b)    

i.  Explain the structure of the FKS scheme and how the construction works. [5 marks]

ii.  State the space usage of the FKS scheme and state the time complexity of the construction. [2 marks]

iii. After the construction is complete, what time complexity guarantees are pro- vided on the operations supported? [1 mark]

(c)  The SubArray-Distinctness problem can be deined as follows: Given an array A containing 2n integers, determine whether there is an 0 ≤ i ≤ n  such that in the subarray A[i . . . i + n — 1], every  integer is unique. I.e. there  is  no 0 ≤ k1 < n and 0 ≤ k2 < n with k1 ≠ k2  such that A [i + k1] = A [i + k2]. The output should be the leftmost i if at least one suitable subarray exists and FALSE otherwise.

Give an algorithm for the SubArray-Distinctness problem. Your solution should use O(n) space and run in O(n) expected time. You should argue that this is the case. You should also prove the correctness of your algorithm. In this part, you may use any algorithms or data structures given in lectures without proof. [5 marks]

Q3 .   

(a)  In the 2D-range search problem using a range search tree, give the time complexity  for constructing the tree. Also give the time complexity for performing one query  when using fractional cascading. [4 marks]
(b)  Explain  how you can  use the range search tree to determine whether a particular point (a; b) is in a given set. What is the time complexity for the query operation? [2 marks]
(c)  The 3D-range search problem is natural extension of 2D-range search which you have seen before. Describe such a 3D-range search tree and set out the main steps that need to be performed to query this data structure eiciently. You do not need to say how the tree would be constructed nor do you need to describe fractional cascading. [4 marks]
(d)  Set out the main steps, without proof but with relevant deinitions, of the reduction from the LCA problem for a tree with n nodes to the ± 1 range minimum query (±1 RMQ) problem. [8 marks]
(e)  State the running time of both the preprocessing and query steps. [2 marks]