Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
ECO00025C
BSc Degree Examinations SPECIMEN PAPER
Economics and Related Studies
Probability and Statistics
1. [5 marks overall] Let
f (x) = x for 0 ≤ x ≤ c.
(a) [3 marks] Determine the value of the constant c such that f (x) can serve as a probability density for the random variable X
(b) [2 marks] Calculate E (X).
2. [10 marks overall] Let X and Y denote two continuous random variables and let
f (x,y) = c (x2 + 4xy, for 0 ≤ x ≤ 1 and 0 ≤ y ≤ 1.
(a) [5 marks] Determine the value of the constant c such that f (x,y) can serve as a density function for X and Y.
(b) [5 marks] Are X and Y independent?
3. [10 marks overall] You have ten coins in your pocket. Nine of them are ordinary coins with equal probability of coming up head or tail and the tenth has two heads.
(a) [5 marks] If you take one of the coins at random from your pocket, what is the probability that it is the coin with two heads?
(b) [5 marks] If you flip the coin now and it comes up head, what is the probability that it is the coin with two heads?
4. [5 marks overall] Let X ∼ N (−1, 4), Y ∼ t(7) and W ∼ χ2 (7)
(a) [2 marks] Compute P (−2 < X < 3).
(b) [1 marks] Compute P (Y > 1.415).
(c) [2 mark] Find c such that P (W ≤ c) = 0.05.
5. [10 marks overall] Let X and Y denote two discrete random variables with joint proba- bility distribution f (x,y)
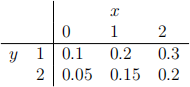
(a) [3 marks] Compute the marginal distributions g (x) and h(y).
(b) [2 marks] Are X and Y independent?
(c) [5 marks] Compute the conditional distribution w (y|X = 1) and E (Y |X = 1) .
6. [15 marks overall] Suppose that you are an expected utility maximiser with a utility function U (x) = x1/2 for x > 0.
(a) [7 marks] What is your certainty equivalent for a gamble that would pay you £50 or £150 with equal probability?
(b) [8 marks] What is your risk premium associated with the gamble ?
7. [15 marks overall] A fellow student claims that the average score on last year’s statistics exam is 65.You suspect it might be lower and draw a random sample of n = 10 exam marks from last year.You find that the average score in your sample is 61.7, with an estimate of the sample standard deviation of 3.6. Assume that the population of scores in last year’s statistics exam is normal.
(a) [4 marks] Explain how you would test the hypothesis that the average score is less than 65, and propose a test statistic for it.
(b) [6 marks] Test the hypothesis you defined in (a) at the 5% significance level and briefly comment on the outcome of the test.
(c) [5 marks] Suppose now that the scores’ population is not normal, but the same average score and sample standard deviation are based on a sample of 100 scores. Explain how you would test the same hypothesis you defined in (a).
8. [15 marks overall] Let X1 denote a rand
sample (of size n = 1) from a Poisson distribution Pois(λ) (0 < λ < ∞) and let λ = X1 denote an estimator for the unknown λ .
(a) [5 marks] Show that 
is an unbiased estimator for λ .
(b) [10 marks] Show that 
is not a consistent estimator for λ .
9. [15 marks overall] In a study designed to examine how the number of hours people spend watching French movies affects their French test scores, a random sample was utilized to estimate the quantitative impact of hours spent watching French movie on the test scores. Denoting by X the number of hours per week spent watching French movies and Y the people’s scores on the French test, the following linear regression model was estimated
Yi = α + βXi + εi
for i = 1, 2, ..., 20 where εi is i.i.d.N(0,σ 2 ). The results of the OLS estimation of the normal linear regression model were
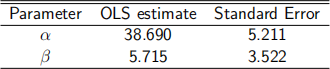
(a) [2 mark] Write down the fitted regression, and comment on the estimate of β .
(b) [1 marks] Predict the test scores of a student with 2 hours study per week.
(c) [9 marks] Test the statistical significance of the slope coefficient at the 10% level of significance.
(d) [3 marks] Compute a 90% confidence interval for β .