CEG5301 Machine Learning with Applications:
Part I: Homework #3
Important note: the due date is 17/03/2024. Please submit the softcopy of your report to the submission folder in CANVAS. Late submission is not allowed unless it is well justified. Please supply the MATLAB code or Python Code in your answer if computer experiment is involved.
Please note that the MATLAB toolboxes for RBFN and SOM are not well developed. Please write your own codes to implement RBFN and SOM instead of using the MATLAB toolbox.
Q1. Function Approximation with RBFN (10 Marks)
Consider using RBFN to approximate the following function:
y = 1.2 sin(πx) 一 cos(2.4πx) , for x E [一1.6, 1.6]
The training set is constructed by dividing the range [一1.6, 1.6] using a uniform step length 0.08, while the test set is constructed by dividing the range [一1.6, 1.6] using a uniform step length 0.01. Assume that the observed outputs in the training set are corrupted by random noise as follows.
y(i) = 1.2 sin(πx (i)) 一 cos(2.4πx(i)) + 0.3n(i)
where the random noise n(i) is Gaussian noise with zero mean and stand deviation of one, which can be generated by MATLAB command randn. Note that the test set is not corrupted by noises. Perform the following computer experiments:
a) Use the exact interpolation method (as described on pages 17-26 in the slides of lecture five) and determine the weights of the RBFN. Assume the RBF is Gaussian function with standard deviation of 0.1. Evaluate the approximation performance of the resulting RBFN using the test set. (3 Marks)
b) Follow the strategy of “Fixed Centers Selected at Random” (as described on page 38 in the slides of lecture five), randomly select 20 centers among the sampling points. Determine the weights of the RBFN. Evaluate the approximation performance of the resulting RBFN using test set. Compare it to the result of part a). (4 Marks)
c) Use the same centers and widths as those determined in part a) and apply the regularization method as described on pages 43-46 in the slides for lecture five. Vary the value of the regularization factor and study its effect on the performance of RBFN. (3 Marks)
Q2. Handwritten Digits Classification using RBFN (20 Marks)
In this task, you will build a handwritten digits classifier using RBFN. The training data is provided in MNIST_M.mat. Each binary image is of size 28*28. There are 10 classes in MNIST_M.mat; please select two classes according to the last two different digits of your matric number (e.g. A0642311, choose classes 3 and 1; A1234567, choose classes 6 and 7). The images in the selected two classes should be assigned the label “1” for this question’s binary classification task, while images in all the remaining eight classes should be assigned the label “0”. Make sure you have selected the correct 2 classes for both training and testing. There will be some mark deduction for wrong classes selected. Please state your handwritten digit classes for both training and testing.
In MATLAB, the following code can be used to load the training and testing data:
-------------------------------------------------------------------------------------------------------
load mnist_m.mat;
% train_data à training data, 784x1000 matrix
% train_classlabel à the labels of the training data, 1x1000 vector
% test_data à test data, 784x250 matrix
% train_classlabel à the labels of the test data, 1x250 vector
|
After loading the data, you may view them using the code below: |
|
tmp=reshape(train_data(:,column_no),28,28); imshow(tmp); |
|
To select a few classes for training, you may refer to the following code: |
|
trainIdx = find(train_classlabel==0 | train_classlabel==1 | train_classlabel==2); % find the location of classes 0, 1, 2 Train_ClassLabel = train_classlabel(trainIdx); Train_Data = train_data(:,trainIdx); |
Please use the following code to evaluate:
-------------------------------------------------------------------------------------------------------
TrAcc = zeros(1,1000);
TeAcc = zeros(1,1000);
thr = zeros(1,1000);
TrN = length(TrLabel);
TeN = length(TeLabel);
for i = 1:1000
t = (max(TrPred)-min(TrPred)) * (i-1)/1000 + min(TrPred);
thr(i) = t;
TrAcc (i) = (sum(TrLabel(TrPred
TeAcc (i) = (sum(TeLabel(TePred
end
plot(thr,TrAcc, ' .- ',thr,TeAcc, '^- ');legend('tr', 'te');
TrPred and TePred are determined by TrPred(j) =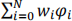 (TrData(: , j)) and TePred(j) =
(TrData(: , j)) and TePred(j) =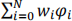 (TeData(: , j)) where N is the number of hidden neurons. TrData and TeData are the training and testing data selected based on your matric number. TrLabel and TeLabel are the ground-truth label information (Convert to {0,1} before use!).
(TeData(: , j)) where N is the number of hidden neurons. TrData and TeData are the training and testing data selected based on your matric number. TrLabel and TeLabel are the ground-truth label information (Convert to {0,1} before use!).
You are required to complete the following tasks:
a) Use Exact Interpolation Method and apply regularization. Assume the RBF is Gaussian function with standard deviation of 100. Firstly, determine the weights of RBFN without regularization and evaluate its performance; then vary the value of regularization factor and study its effect on the resulting RBFNs’ performance. (6 Marks)
b) Follow the strategy of “Fixed Centers Selected at Random” (as described in page 38 of lecture five). Randomly select 100 centers among the training samples. Firstly, determine the weights of RBFN with widths fixed at an appropriate size and compare its performance to the result of a); then vary the value of width from 0.1 to 10000 and study its effect on the resulting RBFNs’ performance. (8 Marks)
c) Try classical “K-Mean Clustering” (as described in pages 39-40 of lecture five) with 2 centers. Firstly, determine the weights of RBFN and evaluate its performance; then visualize the obtained centers and compare them to the mean of training images of each class. State your findings. (6 Marks)
Q3. Self-Organizing Map (SOM) (20 Marks)
a) Write your own code to implement a SOM that maps a 1-dimensional output layer of 40 neurons to a “hat” (sinc function). Display the trained weights of each output neuron as points in a 2D plane, and plot lines to connect every topological adjacent neurons (e.g. the 2nd neuron is connected to the 1st and 3rd neuron bylines). The training points sampled from the “hat” can be obtained by the following code:
x = linspace(-pi,pi,400);
trainX = [x; sinc(x)]; → 2x400 matrix
plot(trainX(1,:),trainX(2,:),'+r'); axis equal
-------------------------------------------------------------------------------------------------------
(3 Marks)
b) Write your own code to implement a SOM that maps a 2-dimensional output layer of 64 (i.e. 8×8) neurons to a “circle”. Display the trained weights of each output neuron as a point in the 2D plane, and plot lines to connect every topological adjacent neurons (e.g. neuron (2,2) is connected to neuron (1,2) (2,3) (3,2) (2,1) by lines). The training points sampled from the “circle” can be obtained by the following code:
-------------------------------------------------------------------------------------------------------
X = randn(800,2);
s2 = sum(X.^2,2);
trainX = (X.*repmat(1*(gammainc(s2/2,1).^(1/2))./sqrt(s2),1,2))'; → 2x800 matrix
plot(trainX(1,:),trainX(2,:),'+r'); axis equal
(4 Marks)
c) Write your own code to implement a SOM that clusters and classifies handwritten digits. The training data is provided in Digits.mat. The dataset consists of images in 5 classes, namely 0 to 4. Each image with the size of 28*28 is reshaped into a vector and stored in the Digits.mat file. After loading the mat file, you may find the 4 matrix/arrays, which respectively are train_data, train_classlabel, test_data and test_classlabel. There are totally 1000 images in the training set and 100 images in the test set. Please omit 2 classes according to the last digit of your matric number with the following rule: omitted class1 = mod(the last digit, 5), omitted_class2 = mod(the last digit+1, 5). For example, if your matric number is A0642347, ignore classes mod(7,5)=2 and mod(8,5)=3; A1234569, ignore classes 4 and 0.
Thus, you need to train a model for a 3-classes classification task. Make sure you have selected the correct 3 classes for both training and testing. There will be some mark deduction for wrong classes selected. Please state your handwritten digit classes for both training and testing.
After loading the data, complete the following tasks:
c- 1) Print out corresponding conceptual/semantic map of the trained SOM (as described in page 24 of lecture six) and visualize the trained weights of each output neuron on a 10×10 map (a simple way could be to reshape the weights of a neuron into a 28×28 matrix, i.e. dimension of the inputs, and display it as an image). Make comments on them, if any. (8 Marks)
c-2) Apply the trained SOM to classify the test images (in test_data). The classification can be done in the following fashion: input a test image to SOM, and find out the winner neuron; then label the test image with the winner neuron’s label (note: labels of all the output neurons have already been determined in c- 1). Calculate the classification accuracy on the whole test set and discuss your findings. (5 Marks)
The recommended values of design parameters are:
1. The size of the SOM is 1×40 for a), 8 ×8 for b), 10×10 for c).
2. The total iteration number N is set to be 500 for a) & b), 1000 for c). Only the
first (self-organizing) phase of learning is used in this experiment. 3. The learning rate η(n) is set as:
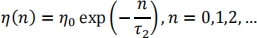
where η0 is the initial learning rate and is set to be 0.1, τ2 is the time constant and is set to be N.
4. The time-varying neighborhood function is:
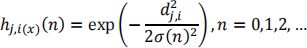
where dj,i is the distance between neuronj and winner i, σ (n) is the effective width and satisfies:

where σ0 is the initial effective width and is set according to the size of output layer’s lattice, τ1 is the time constant and is chosen as 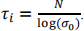
Again, please feel free to experiment with other design parameters which may be different from the given ones.