COMP 550.002: Fall 2023
Assignment 6
Announced: November 22, 2023
Due Date: December 6, 2023
All problems are collaborative. You can form a group of at most four students to collaborate. You MUST mention the names of your collaborators, and cite any material you took help from (including discussions on canvas by other students) except the textbook and provided slides.
CLRS refers Cormen et al. textbook.
Problem 1 (16 Points)
Run the Bellman-Ford algorithm on the directed graph of Fig. 1. In each pass, relax edges in the order of (u,v), (u,x), (u,y), (v, u), (x,v), (x,y), (y, v), (y, s), (s,u), (s,x). Show the d and π values after each pass.
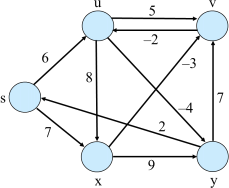
Figure 1: Graph for Problem 1
Consider a directed graph G = (V, E) on which each edge (u,v) ∈ E has an associated value r(u,v), which is a real number in the range 0 ≤ r(u,v) ≤ 1 that represents the reliability of a communication channel from vertex u to vertex v. Interpret r(u,v) as the probability that the channel from u to v will not fail, and assume that these probabilities are independent. Give an efficient algorithm to find the most reliable path between two given vertices.
Problem 3 (16 Points)
Consider the following approach for finding the shortest path from node s to node t in a directed graph with some negative-weight edges: add a large constant to each edge weight so that all the weights become positive, then run Dijkstra’s algorithm starting at node s, and return the shortest path found to node t (using v.π pointers starting from t.π). Is this a valid method? Either prove that it works correctly, or give a counterexample.
Consider the following undirected graph G in Fig. 2. The following two questions ask to run Prim’s and Kruskal’s algorithms on G.
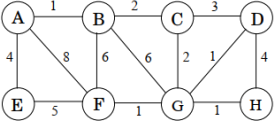
Figure 2: Graph for Problem 4
(a) Assuming A is the starting node, write down the order of the nodes added to the partial spanning tree by the Prim’s algorithm (i.e., order the nodes according to the Extract-Min operation in the Prim’s pseudocode in CLRS). Whenever there is a choice (ties) of nodes, always use alphabetic ordering (e.g., start from node A). Finally, draw the constructed MST.
(b) Write down the order of the edges added to the MST by the Kruskal’s algorithm (i.e., the order in which edges are added in set A in Kruskal’s pseudocode in CLRS). Whenever there is a choice (ties) of edges, always use alphabetic ordering (e.g., since the weights of both (B,C) and (C,G) are 2, pick (B,C) instead of (C,G) as B < C; for (G,H) and (G,D), pick (G,D) as D < H).
Problem 5 (16 Points)
Suppose T isa minimum spanning tree of a graph G = (V, E). Assume that G′ is a graph obtained by adding to G a new vertex and some weighted edges incident to the new vertex. Can you construct a minimum spanning tree of G′ by adding one of the new edges to T. Explain your answer with reasonings.
Problem 6 (15 + 5 = 20 points)
For the flow network in Fig. 3, answer the following questions.
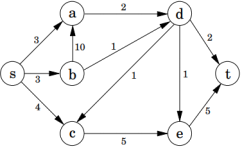
Figure 3: Graph for Problem 6
(a) Show the execution of the Edmonds-Karp algorithm on the flow network of Fig. 3. The numbers along the edges denote edge capacities. Your illustration should be similar to the example execution shown in slides and CLRS.
(b) Determine acut with minimum capacity for the graph in Fig. 3? (Remember that the minimum cut capacity should equal the value of the maximum flow in your answer of (a).)
Problem 7 (Extra Credit: 10 Points)
Suppose you have computed a minimum spanning tree T of a graph G. We want to support
Decrease-Edge-Weight(u,v,c) operation for graph G, that will decrease the weight, w(u,v) of edge (u,v) to c if the current weight of (u,v) is larger than c, and will not change the edge weight otherwise. For example, if the weight of an edge (u,v) is 10, then Decrease-Edge-Weight(u,v,4) will make w(u,v) = 4. Doing such operation may impact the minimum spanning tree (i.e., the tree T may not be a minimum spanning tree of G anymore). Give an algorithm for updating the minimum spanning tree T when a Decrease-Edge-Weight(u,v,c) is performed. Make your algorithm as efficient as you can and mention its time complexity.
Problem 8 (Extra Credit: 15 Points)
[This problem is based on CLRS Problem 24.2-11] The edge connectivity of an undirected graph is the minimum number k of edges that must be removed to disconnect the graph. For example, the edge connectivity of a tree is 1, and the edge connectivity of a cyclic chain of vertices is 2. Show how to determine the edge connectivity of an undirected graph G = (V, E) by running a maximum-flow algorithm on at most |V | flow networks, each having O(V + E) vertices and O(E) edges.