Practice Test 1
DSO 530: Applied Modern Statistical Learning Methods
2024
You have 90 minutes to do the problems. For multiple choice questions (1-16), make sure to read the questions very carefully and write down the best answer. If you write down multiple answers for a question, you will receive zero for that question. For short answer questions (17-22), write concisely, and clearly. This test is open notes. You can read the class slides, notes, and python tutorials as printouts or on your computer, but you should not search on-line, open jupiter notebooks or use Python, watch class recordings, or use ChatGPT and other AI tools. Questions 1, 17-22 are worth 2 points each, and the rest are worth 1 point each. The total points are 29. Do not write your answers on this test paper. Instead, write your answers on some blank papers. For both multiple choice and short answer questions, you should clearly indicate the correspondence between the question number and your answer. All answers have to be hand-written. Do not upload your scratch paper.
If you have multiple pages in your answers, number these pages. Write down your name (Last, First) and USC Student ID number on top of every page of your answers.
submission instructions: Scan your answers into a single pdf document. Name this document by lastname_firstname_uscIDnumber_test1.pdf. Then, upload this pdf file to Blackboard (like you did for HW1 and Quiz1). Finally, send a public message on Zoom to sign off. For example: Alex James signs off at 8:15 pm. Note that after you sign off, any submission to Blackboard will be considered as improper conduct.
additional instructions: Do not redistribute this test. If you download the test, delete it after you submit your answers. Also, do not discuss or share your answers after the test.
part a) multiple choices
1. Let X be a standard normal random variable (i.e., X ≥ N (0, 1)), and Z be a uniform random variable between 0 and 1 (i.e., Z ≥ Uniform(0, 1)). Which of the following is/are correct?
i) X is a discrete random variable and Z is a continuous random variable
ii) P(X = 0) > P(Z = 0.5)
Choose one of the follwoing:
• A) i)
• B) ii)
• C) i) and ii)
• D) Neither i) nor ii)
2. How many of the following statements is/are correct?
i) Disjoint events are independent.
ii) R2 is never larger than 2.
iii) In statistical hypothesis test, we reject the null hypothesis if p-value is larger than α.
iv) Correlation measures the linear dependency between two categorical variables.
Choose one of the follwoing:
• A) None
• B) One
• C) Two
• D) Three
• E) Four
Questions 3 — 8 are based the Housing dataset. As we have seen this dataset multiple times in lectures and tutorials, we will skip the description.
import numpy as np
import pandas as pd
housing = pd.read_csv("Housing.csv")
housing.info()

3. Based on the above information, how many observations are there in the Housing dataset?
• A) 506
• B) 64
4. If we were to predict the medv using three features in the dataset, how many linear regression models can we potentially consider?
• A) 506
• B) 5
• C) 20
• D) 10
5.
import statsmodels.formula.api as smf
result1 = smf.ols('medv ~ river + ptratio', data=housing).fit()
result1.summary()
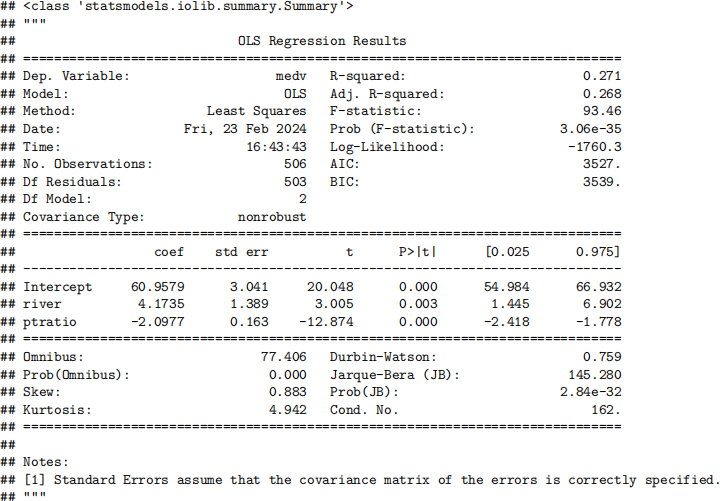
What percentage of the variation of the response does the regression explain?
• A) 27.1%
• B) 0
• C) 1
• D) We are not given proper output to decide.
6.
x_new = {'river': [0, 1], 'ptratio': [10, 16]}
x_new_df = pd.DataFrame(x_new)
prediction1 = result1.get_prediction(x_new_df)
prediction1.summary_frame()
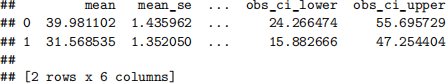
In the above implementation, we predicted the medv for two neighborhoods. The first neighborhood has river = 0, and ptraio = 10, and the second one has river = 1 and ptratio = 16. Which neighborhood has a higher predicted medv?
• A) First
• B) Second
7. Now regress medv on river, ptratio and zn. Do you expect a higher (in-sample) R2 than what you got for regressing medv on river and ptratio only?
• A) Yes
• B) No
8. Suppose we want to randomly split housing into training and test parts with 30% as the test data. You split the data twice, both using the train_test_split function from sklearn.model_selection. For the first split, you set random state equals 0; and for the second split, you also set random state equals 0. Do you expect that the training data sets from these two splits are the same?
• A) Yes
• B) No
9. Let h be a classifier for binary classification and P(h(X) ≠ Y ) denotes its classification error. Recall that P(h(X) ≠ Y |Y = 0) is type I error and P(h(X) ≠ Y |Y = 1) is type II error. Then
• A) P(h(X) ≠ Y ) = type I error + type II error.
• B) P(h(X) ≠ Y ) = type I error · P(Y = 0) + type II error · P(Y = 1)
• C) P(h(X) ≠ Y ) = type I error · P(Y = 1) + type II error · P(Y = 0)
10. KNN classifier does not assume a probabilistic model.
• A) The statement is true.
• B) The statement is false.
11. Which of the following statement(s) about logistic regression is/are correct?
• i) Logistic regression and linear discriminant analysis are the same.
• ii) One usually uses the least squares approach to fit logistic regression model.
Choose one of the follwoing:
• A) i)
• B) ii)
• C) i) and ii)
• D) neither i) nor ii)
12. For KNN classifier, choosing K = 1 would lead to training error equal to 0. But this choice is usually
• A) bad, because it leads to overfitting
• B) good, because this training error exactly what we want.
Questions 13 — 15 are based an email spam data. For simplicity, one can think of the first 57 columns as engineered features from the original emails, while the last column indicates whether an email is spam (class 1) or non-spam (class 0). There are 1813 spam emails. There is no missing data in this dataset.
df_spam = pd.read_csv("spambase.data", header = None)
df_spam.shape
13. How many non-spam emails are there in this dataset?
• A) 1813
• B) 2788
• C) 4601
14. If we train logistic regression on this dataset, the default threshold of the fitted signoid function is 0.5. If we increase the threshold from 0.5 to 0.6, how will type I error change?
• A) Increase
• B) Decrease
• C) Changing the threshold should not have any impact on type I error.
15. We want to split the email spam data into the training and test sets. Should we specify stratify=y in train_test_split?
• A) Yes, because we are dealing with a classification problem
• B) No, because we are dealing with a regression problem
16. Which of the following is true about supervised learning?
• A) AUC is the only thing people care in evaluating classifiers’ performance.
• B) A classifier that is in the lower right half of the ROC space is inferior to some random guess.
• C) In linear regression, out-of-sample R2 can be greater than 1.
part b) short answer questions
17. Suppose in the population, there are 5% of the people using Drug D. Scientists have developed a test to identify the users of this drug. This test has false negative rate 5% and false postive rate 5%. Then given that a person is tested positive, what is the probability that this person is a drug D user? (Show your calculation in addition to the final answer)
18. We ran simple linear regression on a training dataset, and obtained the regression line: y = 1+ x. Supposse the test data only consists of three (x, y) pairs: {(0, 1),(2, 3),(5, 6)}. What is the out-of-sample R squared? (Show your calculation in addition to the final answer)
19. The ROC space is a unit square (recall that the ehorizontal axis is for type I error, and the vertical axis is 1-type II error). Draw an ROC space and label two points that represent respectively “perfect classification”, and a random guess classifier with type I error 0.05 (and type II error 0.95).
20. Write down logistic regression model with three independent variables
21. Write down the Bayes classifier for binary classification. Does the Bayes classifier usually achieve 0 classification error? (For the second part, a simple Yes or No answer suffices.)
22.
X = [[1, 2, np.nan], [3, 4, 3], [8, 7, 5], [8, 9, 7]]
df = pd.DataFrame(X, columns=['A', 'B', 'C'])
df
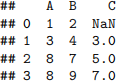
There is one missing value in the C column. To use KNNImputer with k = 2, we need to calculate the distance between the 0th row and other rows. Denote the squares of these distances by d2(0, 1), d2(0, 2) and d2(0, 3). Please find d2(0, 1), d2(0, 2) and d2(0, 3). Show the steps as well as the final results. (Hint: Tutorial 2)