Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
ECON0051 Economics of Regulation
Sample Exam Question No. 1
AY2023/24
Question on Topic '(Quantity) Regulation of a Monopolist with Hidden Information' Consider the following simple version of the regu- lation model with demand uncertainty studied by Basso, Leonardo J., Nicol·s Figueroa, and Jorge V·squez (2017): ''Monopoly Regulation under Asym- metric Information: Prices versus Quantities'', The RAND Journal of Eco- nomics, Vol. 48, No. 3, pp. 557ñ578.
In particular, the monopoly firm has private information about consumer demand, as captured by a parameter θ 2 [0; 1]. The inverse demand function is P (q; θ) = a + θ 一 bq where θ is a demand shock parameter. The firm observes θ, which is its private information, while the regulator does not. However, the regulator has a prior belief about θ captured by a cumulative distribution function G (θ; Y) with density g (θ; Y) 三 G0 (θ; Y) = Y (1 一 θ)y — 1 for Y > 1. The Örmís cost function is C (q) = cq with c > 0.
The regulator wishes to design an incentive compatible and expected welfare-maximizing quantity-mechanism which (as derived in Tutorial 4 - you do not have to repeat this derivation here) consists of a non-decreasing assignment rule q (θ) 2 R+ and a lump-sum transfer rule T (θ) 2 R where:
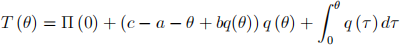
Such a menu fq (θ) ; T (θ)gθ2[0;1] induces truthful revelation by the firm for all realizations of θ. The regulator chooses the details of this menu so as to maximize the expected value of social welfare, which is given by the weighted sum of net consumer surplus and the firm's profit, where a weight of a 2 [0; 1] is applied to firm profits: CS (q (θ)) 一 T (θ) + aⅡ (θ). The regulator must also account for the firm's particiation constraint: Ⅱ (θ) > 0 for all θ 2 [0; 1].
(a-1) [50 points] Use the above information about the incentive compat- ible transfer schedule T (θ) to express the regulatorís expected social welfare in terms of the assignment schedule q (θ), demonstrating that it takes the form:
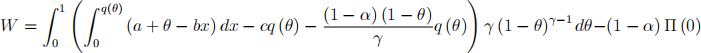
Then maximize W pointwise to obtain the optimal assignment schedule q* (θ) and the optimal profit-level Ⅱ (0) of the lowest type.
(a-2) [10 points] How do the regulated price and quantity schedule change if the regulatorís belief about the firm's demand becomes less 'favourable' in the sense that it considers lower demand shocks more likely (Hint : an increase in the parameter Y shifts more probability mass of the distribution g (θ; Y) towards lower realizations of the demand shock θ). What happens in the limit as Y becomes arbitrarily large? Interpret your findings!
(b) [40 points] Compare the optimal quantity schedule q* (θ) with the first-best regulation mechanism (the one that would be used by the regulator it the firm's type θ was observable, as described by Definition 2 in Basso et al. (2017)). Explain why you think the optimal schedule q* (θ) distorts the firm's output quantity downwards, and especially so for low realizations of the demand shock θ? In particular, discuss the incentive problem that would arise if a firm with private information about its type θ were asked by the regulator to produce the first-best quantity qFB (θ).