ELEC9731, 2024, Term 1, Take Home Exam
due – Monday 29/04/2024 17:00 (Sydney time).
Question 1 (16 marks, Dorfman, Bishop). Consider the control system of Fig. 12.1 of Lecture Notes with
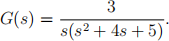
Design a PID controller to achieve
(a) an acceleration error constant Ka = 2;
(b) a phase margin equal to
;
(c) a bandwidth greater than 2.8 rad/s.
Select an appropriate pre-filter and plot the response to a step input.
Reminder: acceleration error constant is the constant Ka such that the steady state error to a parabolic input, r(t) = 0.5t 2 is equal to
.
Question 2 (18 marks). Consider the following scalar discrete-time control sys-tem
x(k + 1) = −5x(k) + 4u(k)
where x ∈ R, u ∈ R and x(0) = −2. Let N > 1 be some integer.
(a) Consider the following cost function

Find the optimal control law and the minimal cost.
(b) Consider the following cost function

Find the optimal control law and the minimal cost.
(c) Consider the following cost function

Find the optimal control law and the minimal cost.
(d) Consider the cost function from (c) and the constraint |u(k)| ≤ 3 for all k. Find the optimal control law and the minimal cost.
Question 3 (16 marks). Consider the continuous-time linear system with the disturbance input w(t) and the measured output y(t) where the transfer function T(s) from w to y is

Also, we assume that there is a measurement noise input v(t).
(a) Obtain a state-space model for this system.
(b) Is this system stable?
(c) Assume that
(t) and
(t) are white-noise processes. Take some sensible impulsive correlation matrices Q and R and generate a Kalman filter for estimating the states of the system.
(d) Generate an H∞ filter to estimate the states of the system.
(e) Simulate the plant and the filters from (c) and (d) for various types of w(t) and v(t), e.g. white noises, sinusoidal inputs, some other deterministic functions. Compare the performance of the filters.