EC404: Macroeconomics for MRes
Problem Set 2: Overlapping Generation Model
1. Consider the OLG economy discussed in the lectures where there is no ex-ogenous technological growth (g = 0). Let n denote the rate of population growth. Assume households have a CRRA utility function with risk aversion parameter σ, such that they maximise
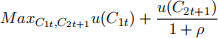
subject to
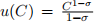, St denotes savings, ρ > 0 is the discount rate, and rt+1 the real rate of return on savings.
(a) Derive the Euler equation of the households in this economy. Explain intuitively your answer.
(b) Show that when σ < 1 an increase in the interest rate yields an increase in savings St . Why when the utility is logarithmic σ = 1 savings do not respond to changes in the interest rate? Explain intuitively your answer. [10 marks]
(c) Assume that the production function is Cobb-Douglas such that 
, where α denotes the capital share in output and A is a constant. Also assume that σ = 1 such that the utility function becomes logarithmic. Show that in this economy the law of motion for capital per worker is given by
(d) Show that the above law of motion of capital implies that the economy will converge to a steady state if the economy starts with a level of k0 > 0. Graph your answer and explain intuitively your result.
2. Consider the OLG economy discussed in the lectures where there is no ex-ogenous technological growth (g = 0). Let n denote the rate of population growth. Assume households have a logarithmic utility function, such that they maximise
subject to
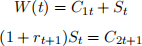
where St denote savings, ρ > 0 is the discount rate, rt+1 the real rate of return on savings. Assume that the production function is Cobb-Douglas such that 
, where α denotes the capital share in output and A is a constant and normalized to 1.
(a) Show that in this economy the law of motion for capital per worker is given by
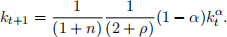
(b) Pay-as-you-go social security: Suppose the government taxes each young individual an amount T and uses the proceeds to pay benefits to old individuals; thus each old person receives (1 + n)T. How, if at all, does this change affect the equation describing the evolution of kt shown in part (a). How, if at all, does this change affect the balance-growth-path value of k?
(c) Fully funded social security: Suppose instead that the government taxes each young person an amount T and uses the proceeds to pur-chase capital. Individuals born at t therefore receive (1 + rt+1)T when they are old. How, if at all, does this change affect the equation de-scribing the evolution of kt shown in part (a). How, if at all, does this change affect the balance-growth-path value of k?
(d) Use your answers in parts (b) and (c) to explain the differences between pay-as-you-go and fully funded social security systems.