EC404: MRes Macroeconomics
Problem Set 1: Solow
Oct 2021
1. Consider the following production function:
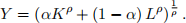
It is called constant elasticity of substitution (CES) production function.
(a) Show that this production function is constant return to scale.
(b) Introduce technologies into the production function:
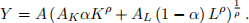
Show that A is neutral: It increases MPK (marginal productivity of capital dY/dK) and MPL equally in terms of percentage changes.
(c) Show that AK may not be neutral: It may increase MPK more than MPL in terms of percentage changes, i.e., capital biased. Find the conditions for ρ under which AK is capital biased.
(d) * Show that if ρ ! 0, then the CES production function converges to Cobb-Douglas.
2. Consider an economy on its balanced growth path that is characterised by the Solow growth model and by the fact that there is technological progress and no population growth. Now suppose there is a one-time jumpin the number of workers.
(a) At the time of the jump, does output per unit of effective labour rise, fall, or stay the same? Why? Explain your answer. [5 marks]
(b) After the initial change (if any) in output per unit of effective labour when the new work- ers appear, is there any further change in output per unit of effective labour? If so, does it rise or fall? Why? Explain your answer. [10 marks]
(c) Once the economy has again reached a balanced growth path, is output per unit of effec- tive labour higher, lower, or the same as it was before the new workers appeared? Why? Explain your answer. [10 marks]
3. Suppose the world consists of two regions, the “North” and the “South” . Output and capi- tal accumulation in region i (i = N, S) are given by Yi(t) = Ki(t)α [A i(t)(1 - aLi )Li]1-α
and K˙i(t) = siYi(t). New technologies are developed in the North. Specifically, A(˙)N (t) = BaLNLNAN(t). Improvements in Southern technology, on the other hand, are made by learn-ing from Northern technology: A˙S (t) = μaLSLS[AN(t) - AS(t)] if AN(t) > AS(t); other-wiseA˙S (t) = 0. Here aLN is the fraction of the Northern labor force engaged in R&D, and aLS is the fraction of the Southern labor force engaged in learning from Northern technology; the rest of the notation is standard. Note that LN and LS are assumed constant.
(a) What is the long-run growth rate of the Northern output per worker? [5 marks]
(b) Define Z(t) = AS(t)/AN (t). Find an expression for Z(˙) as a function of Z and the parameters of the model. Is Z stable? If so, what value does it converge to? What is the long-run growth rate of Southern output per worker? [10 marks]
(c) Assume aLN = aLS and sN = sS . What is the ratio of output per worker in the South to output per worker in the North when both economies have converged to their balanced growth paths? [10 marks]