CSCE 551/MATH 562, Homework 1
due Monday 1/30/2023
The numbered exercises are from the textbook, written out for the purpose of comparing your book version’s exercises with mine. (Note: “state diagram” is the same as “transition diagram.”) You must do the exercises as worded below.
Exercise 1.4: Each of the following languages is the intersection of two simpler languages. In each part, construct DFAs for the simpler languages, then combine them using the construction discussed in footnote 3 (page 46) to give the state diagram of a DFA for the language given. In all parts, Σ = {a, b}.
c. {w | w has an even number of a’s and one or two b’s}
e. {w | w starts with an a and has at most one b}
Exercise 1.5: Each of the following languages is the complement of a simpler language. In each part, construct a DFA for the simpler language, then use it to give the state diagram of a DFA for the language given. In all parts, Σ = {a, b}.
d. {w | w is any string not in a
∗b
∗}
f. {w | w is any string not in a
∗ ∪ b
∗}
Exercise 1.6: Give state diagrams of DFAs recognizing the following languages. In all parts, the alphabet is {0, 1}.
c. {w | w contains the substring 0101 (i.e., w = x0101y for some x and y)}
l. {w | w contains an even number of 0’s or contains exactly two 1’s}
Exercise 1.7: Give state diagrams of NFAs with the specified number of states recognizing each of the following languages. In all parts, the alphabet is {0, 1}.
b. The language of Exercise 1.6c with five states
c. The language of Exercise 1.6l with six states
Exercise 1.16: Use the construction given in Theorem 1.39 to convert the following two nondeterministic finite automata to equivalent deterministic finite automata.
b. [Given in tabular form:]

Not in Textbook 1: Consider the DFA A (below left) over the alphabet {0, 1}:
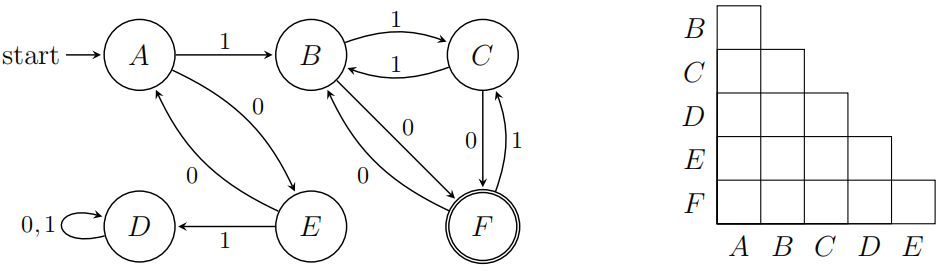
1. Fill in the distiguishability table to the right with X in each entry corresponding to a pair of distinguishable states.
2. Draw (as a transition diagram) the minimal DFA equivalent to A.
Not in Textbook 2: Consider the following DFA A (given in tabular form):
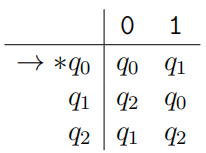
Show that L(A) is the language of all binary representations of natural numbers that are multiples of 3. (Here we assume ε represents the number zero, which is a multiple of 3.) Hint: Prove the stronger statement that, for k ∈ {0, 1, 2}, the computation of A on input string w ends in state qk iff w represents a number whose remainder is k when divided by 3. Make this argument by induction on |w|.