CHE 110B
Midterm Exam 1 – Due 7 February 2024
2024W
‖ Chemistry 110B midterm exam 1
This exam covers electronic structure, computational chemistry, and group theory. It is due on Canvas by 11:59 pm on Wednesday, 7 February 2024; late submissions within an hour of the deadline will forfeit any extra credit from homework score, and submissions afterwards will receive a 0. All times are Pacific. Here are the ground rules (see the FAQs on Canvas for a more complete list):
No collaboration The exam is for you to work on individually. Communicating with other people about the exam questions, whether or not they are in the class, is not allowed. Using any online forums or Q&A services is expressly prohibited, and posting exam content to the internet or viewing answers submitted in response to exam material uploaded online will result in an SJA referral.
Online resources You may use any resources that I have posted to Canvas for the exam, along with the course textbook and your own notes. I strongly discourage searching the internet for general information, as this could potentially run afoul of the “no collaboration” policy if you come across forum posts or similar that pertain to the exam material. However, Google etc. are not prohibited. You may also use online resources I have introduced to you, such as the Basis Set Exchange, the Otterbein Symmetry Gallery, and online character tables.
Questions If you need to ask a question about the exam, you may email me (my email address is at the bottom of the page) or send me a direct message on Discord. I may post clarifications on Discord as well, so please keep an eye out.
To avoid potentially being late due to network issues, do not wait until the last minute to upload your exam! I strongly recommend planning to finish the exam early enough that you have time to go somewhere with reliable internet should that become necessary. We will not have class during the exam time. Good luck!
The questions on this exam are based on Pandey et al. “Resolving the Experimental Photoelectron Spectra of CAl3 Si – ” (J. Phys. Chem. A 2024, 128, 355–369), a copy of which is available on Canvas under the Midterm 1 folder.
1) Write the full Hamiltonian for CAl3 Si and for CAl3 Si – . You may use summation notation, but be explicit about how many terms are in each sum. (12 pts)
2) Write the single-electron, Born-Oppenheimer Hamiltonian for CAl3 Si and for CAl3 Si – . Write all terms explicitly. For the nuclei, use the atom numbers shown in Figure 1 of the paper. (12 pts)
3) Write the Slater determinants for CAl3 Si and CAl3 Si – . There are no degenerate molecular orbitals. For these determinants, fill out 2×2 blocks in each of the 4 corners (i.e., you will write out 16 terms in each determinant). (12 pts)
4) The authors used the aug-cc-pVTZ basis set for geometry optimizations. How many total GTOs are in this basis set for CAl3 S? (10 pts)
5) How many MOs did the authors calculate for CAl3 S (in the same basis set)? (10 pts)
6) Equation 6 in the paper refers to the calculation of matrix elements that look like ⟨ψ1 |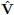 
|ψ2 ⟩, where |ψ1 ⟩ and |ψ2 ⟩ are electronic states and 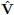is a vibrational coupling operator. For each pair of states listed in Table 3 of the paper, determine the symmetry of 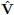for which ⟨ψ1 | 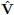|ψ2 ⟩ may be nonzero.
Enter your answers in a form like the table below. (16 pts)
7) Consider only the s orbitals in the aug-cc-pVTZ basis set. Determine how many CAl3 Si MOs of each symmetry are formed from these orbitals. Assume the molecule lies in the xz plane, and use the C2v character table below. (8 pts)
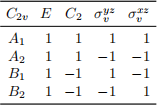
8) Using only the valence p orbitals in a minimal basis , determine all SALCs for CAl3 Si that have A2 symmetry. (20 pts)