Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
MAST20004 Assignment 4, S1 2024: Due 4 pm, Friday 17 May
Question 1
Let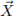 
= (X1, X2) be a bivariate normal random variable with mean vector 
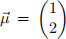and covariance matrix
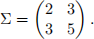
(a) Give an expression for the density function of (X1, X2) (you may wish to look this up on wikipedia) in terms of 
and Σ.
(b) Find the marginal density function of X1.
(c) Find the conditional density fX1|X2 (x|y) for y = 2
(d) Find the variance of the random variable X1 + X2.
(e) Are X1 and X2 independent? Why or why not?
(f) Estimate P(X1 > 2) and P(X1 > 2|X2 > 2) via simulation (show your R code)
Question 2
Let N be a geometric random variable with parameter p, taking values in N. Let X1, X2, . . . be independent Exponential random variables with parameter 2, that are also independent of N. Let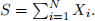 
(a) Find E[S|N = n].
(b) Using your answer to the previous part, find E[S].
(c) What is the distribution of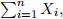 
when n ∈ N?
(d) Find the distribution of S. (Hint: Use conditional expectation to derive the moment generating function of S.)
(e) Using your answer to the previous part, find E[S].
Question 3
Let U1, U2, . . . be independent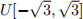 
random variables. For i ∈ N let Wi = Ui + Ui+1.
(a) Find the moment generating function of U1. (Hint: consider the cases where t ≠ 0 and where t = 0 separately).
(b) Use the answer to part (a) to show that E[U1] = 0.
(c) Find Cov(Wi , Wi+1).
(d) let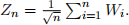 
Show that Zn converges in distribution to some random variable Z, and determine the distribution of Z. (Hint: the Ui random variables are independent of each other).
Question 4
Let X1 and X2 be independent Poisson random variables with parameters λ1 and λ2 respectively and let Y = X1 + X2.
(a) Find E[Y |X1] and Var(Y |X1).
(b) Use your answers to part (a) to find Var(Y ).