Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
EE3025 - Statistical Methods in ECE
Spring 2024
Homework 5
Due on: Tuesday, March 19, 10:00 PM
Problem 1
You are offered to play the following game. You roll a fair die once and observe the result which is shown by the random variable X. At this point, you can stop the game and win X dollars. You can also choose to roll the die for the second time to observe the value Y . In this case, you will win Y dollars. Let W be the value that you win in this game. What strategy do you use to maximize E[W]? What is the maximum E[W] you can achieve using your strategy?
Hint: A natural strategy to choose is the folloing: if X > α then, stop the game after the first roll, otherwise go for the second roll. What should be α?
Problem 2
Let the cdf of a continuous random variable X is given by
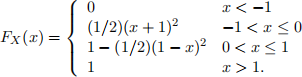
(a) Draw this function, and justify that it is a valid cdf.
(b) what is the pdf of X? sketch it.
(c) What is P[X ≤ 0]? How about P[X > 4/1]?
(d) Compute P[−1/2 < X ≤ 1/2].
Problem 3
Let X ∼ N (0, σ2 ) be a Gaussian random variable.
(a) What are E[X] and E[X2 ]? You do not need to compute them. Rather you can just find them from distribution parameters.
(b) Compute E[|X|].
Hint: Use a change of variable y = 2σ2/x2.
(c) Compute E[X3] and E[X5]. What can you conclude?
(d) Compute E[X4].
Hint: Apply a change of variable y = x2, and use integration by parts.
(e) Let σ = 2. Compute P[X < 5] and P[−1 ≤ X ≤ 2].
Hint: You may use tables for Φ function.
Problem 4
Let Z be an exponential random variable with Var[Z] = 25.
(a) What is the pdf of Z?
(b) What is the second moment of Z?
(c) What is the probability that Z is greater than it’s first moment?
(d) Let Y = 2Z. Find P[Y ≤ k] as a function of k, and from which find the p.d.f. of Y .
Problem 5
Consider the generalized density
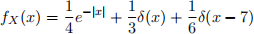
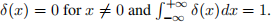
(a) Compute P(0 < X ≤ 7).
(b) Compute P(X = 0).
(c) Compute E[X2].