AS.440.618 Microeconometrics
[Cross Section and Panel Analysis]
Spring 2024
Problem Set #1
Due: Sunday, February 18, at 11:59PM as an upload to Canvas
Instructions: Your problem set will be graded out of 100 points. This problem set will give you in-depth practice working with IV models. You may work on it collaboratively with other members from the class, but I expect each student to write their own solution, in their own words, using their own STATA do-files, etc.
Please refer my syllabus for details on how to submit this one. Otherwise, I reserve the right to deduct up to 10 points off your final score for not following these guidelines.
Theoretical Problems:
1. To investigate the determinants of SAT score, you estimated the equation below:
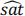 = 1028.1 + 19.3ℎsize − 2.19ℎsize! − 45.09female − 169.81black
= 1028.1 + 19.3ℎsize − 2.19ℎsize! − 45.09female − 169.81black
(6.29) (3.83) (0.53) (4.29 (12.71)
+62.31female × black
(18.15)
n = 4137 R2 = 0.0858
The variable sat is the combined SAT score, hsize is the size of student’s high school graduating class in hundreds; female is a gender dummy variable; and black is a race dummy variable equal to 1 for blacks and zero otherwise.
a. (8 points) Do you see strong evidence that ℎsize! should be included in the model? Based on this estimated equation, what is the optimal high school size?
b. (7 points) If we hold hsize constant, what is the estimated difference in SAT score between nonblack females and nonblack males? How statistically significant is this estimated difference?
c. (7 points) What is the estimated difference in SAT score between nonblack males and black males? Test the null hypothesis that there is no difference between their scores, against the alternative that there is a difference?
d. (8 points) What is the estimated difference in SAT score between black females and nonblack females? What would you need to do to test whether the difference is statistically significant?
2. In a 1995 article “Finishing High School and Starting College: Do Catholic Schools Make a Difference” in The Quarterly Journal of Economics, Bill Evans and Bob Schwab studied the effects of attending a Catholic high school on the probability of attending college. Let College be a binary variable equal to unity if a student attends college and zero otherwise. Let CathHS be a binary variable equal to one if the student attends a Catholic high school. A linear regression model:
College = β0 + β1cathHS + otheT FactoTS + u,
Where the other factors include gender, race, family income, and parental education.
a. (5 points) Why might CathHS to be correlated with u?
b. (5 points) Evans and Schwab have data on a standardized test score taken when each student was a sophomore. What can be done with this variable to improve the causal effect estimate of attending a Catholic high school?
c. (5 points) Let CathRel be a binary variable equal to one if the student is Catholic and zero otherwise. Discuss the two requirements needed for this to be a valid IV for CathHS in the regression. Which of these can be tested?
d. (5 points) Not surprisingly, being Catholic has a significant positive effect on attending Catholic high school, do you think CathRel is a convincing IV for CathHS?
Empirical Problems:
How does fertility affect labor supply? That is, how much does a woman’s labor supply fall when she has an additional child? In this exercise you will estimate this effect using data for married women from the 1980 U.S. Census. The data are available in the file fertility.dta and described in the file Data_Description_PS1.pdf. The data set contains information on married women aged 21–35 with two or more children. (Note: use of outreg2 is not required for this question, but I do ask that you please copy/paste any relevant STATA output into your Word write up.)
a. (5 points) Regress weeksworked on the indicator variable morekids, using OLS. On average, do women with more than two children work less than women with two children? How much less?
b. (5 points) Explain why the OLS regression estimated in (a) is inappropriate for estimating the causal effect of fertility (morekids) on labor supply (weeksworked).
c. (5 points) The data set contains the variable samesex, which is equal to 1 if the first two children are of the same sex (boy–boy or girl–girl) and equal to 0 otherwise. Are couples whose first two children are of the same sex more likely to have a third child? Is the effect large? Is it statistically significant?
d. (5 points) Explain why samesex is a valid instrument for the instrumental variable regression of weeksworked on morekids. Be specific and show any relevant evidence that proves that both the relevance condition and exclusion restriction are satisfied.
e. (7 points) Is samesex a weak instrument? Explain your answer, showing any relevant work.
f. (7 points) Run the reduced form model version of (a). Based on (f) and your work above, derive the IV estimate of this model where samesex is used as an instrument.
g. (8 points) Estimate the regression of weeksworked on morekids, using samesex as an instrument. How large is the fertility effect on labor supply?
h. (8 points) Do the results change when you include the variables agem1, black, hispan, and othrace in the labor supply regression (treating these variables as exogenous)?
Explain why or why not.